Na imagem a seguir (fora de escala) estão representados, em um memo plano, os semicírculos de raios 

Em uma estação de tratamento de água dois reservatórios têm o formato cilíndrico, um com raio de 2 metros e o outro com raio de 3 metros. Os dois reservatórios estavam com 36.000 litros de água cada e foram retirados 3.000 litros de cada um ao longo do dia. Ao final do dia, a diferença entre as alturas das colunas de água desses reservatórios, em cm, é de,
(Dado: use a aproximação π = 3)
Para inscrever um cilindro circular reto, de volume máximo, em um cone de 24 cm de altura e 8 cm de raio da base, deve‐se avaliar a função V(r) = 3 πr2(8-r), 0 .Nesse caso, o volume máximo é igual a 
Uma esfera de raio R está inscrita em um cilindro. O volume do cilindro é igual a:
Uma fábrica de refrigerante resolveu aumentar em 20% a altura de suas latinhas de refrigerantes, porém mantendo o volume. Qual deve ser em porcentagem a diminuição do raio da latinha aproximadamente para que o volume continue o mesmo?
Qual o volume de um cilindro com circunferência de C= 31,4 cm, e altura de 8 cm? Considere π = 3,14.
O maior volume possível de um cilindro circular reto contido em uma esfera de raio R é
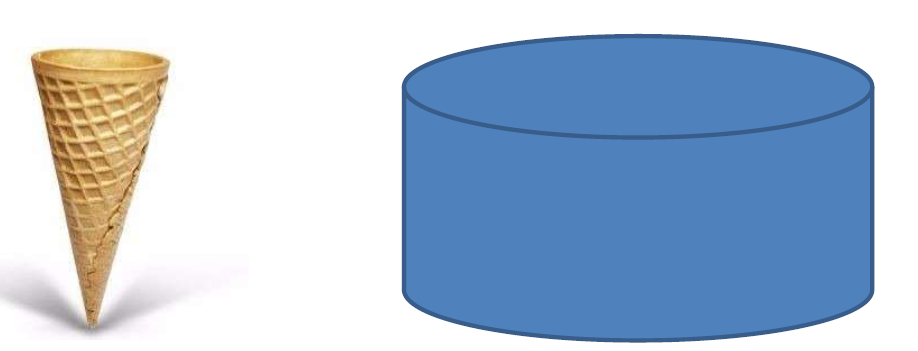
Uma sorveteria vende sorvetes com casquinhas que tem a forma de cone de 5cm de diâmetro e 7cm de profundidade. As casquinhas são totalmente preenchidas de sorvete e, ainda, nelas é superposta uma meia bola de sorvete de mesmo diâmetro do cone. O recipiente onde é armazenado o sorvete tem forma cilíndrica de 22 cm de diâmetro e 6cm de profundidade. O número de casquinhas que podem ser servidos com o sorvete armazenado em um recipiente cheio é de aproximadamente:
Qual é o volume de uma lata de óleo perfeitamente cilíndrica, cujo diâmetro é 8 cm e a altura é 20 cm? (use π=3)
Duzentos litros de um suco serão armazenados em latas cilíndricas de diâmetro 10 cm e altura 13 cm. Cada lata deverá ser preenchida 80% da sua capacidade. A quantidade mínima de latas que serão necessárias para o armazenamento é de aproximadamente:
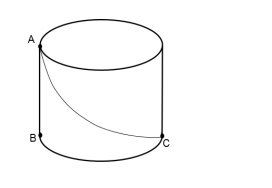
Na superfície de um cilindro reto, o ponto A está no círculo da base superior e os pontos B e C estão no círculo da base inferior.
O segmento AB corresponde à altura do cilindro e o ponto C está diametralmente oposto ao ponto B. Uma formiga parte do ponto
A em direção ao ponto C, caminhado sobre a surperfície do cilindro. Sabendo que a altura e o raio da base do cilindro são iguais a 1,
a menor distância a ser percorrida pela formiga é:
Uma esfera está inscrita num cilindro equilátero cuja área lateral mede 16π cm². O volume da esfera inscrita é
O administrador de uma cidade, implantando uma política de reutilização de materiais descartados, aproveitou milhares de tambores cilíndricos dispensados por empresas da região e montou kits com seis tambores para o abastecimento de água em casas de famílias de baixa renda, conforme a figura seguinte. Além disso, cada família envolvida com o programa irá pagar somente R$ 2,50 por metro cúbico utilizado.
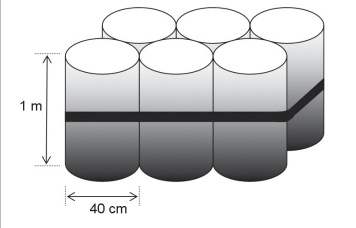
Uma família que utilizar 12 vezes a capacidade total do kit em um mês pagará a quantia de (considere π ≅ 3)
Um fabricante de creme de leite comercializa seu produto em embalagens cilíndricas de diãmetro da base medindo 4 cm e altura 13,5 cm. O rótulo de cada uma custa R$ 0,60. Esse fabricante comercializará o referido produto em embalagens ainda cilíndricas de mesma capacidade, mas com a medida do diãmetro da base igual à da altura. Levando-se em consideração exclusivamente o gasto com o rótulo, o valor que o fabricante deverá pagar por esse rótulo é de
Numa feira de artesanato, uma pessoa constrói formas geométricas de aviões, bicicletas, carros e outros engenhos com arame inextensível. Em certo momento, ele construiu uma forma tendo como eixo de apoio outro arame retilíneo e rígido, cuja aparência é mostrada na figura seguinte:
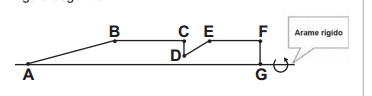
Ao girar tal forma em torno do eixo, formou-se a imagem de um foguete, que pode ser pensado como composição, por justaposição, de diversos sólidos básicos de revolução.
Sabendo que, na figura, os pontos B, C, E e F são colineares, AB = 4FG, BC = 3FG, EF = 2FG, e utilizando-se daquela forma de pensar o foguete, a decomposição deste, no sentido da ponta para a cauda, é formada pela seguinte sequência de sólidos: