Um tesouro foi escondido em uma região plana e o mapa que permite localizar esse tesouro é o seguinte: “A partir da torre de transmissão de energia, ande 30 passos a leste; depois, 10 passos a norte e 25 passos a oeste. Caminhe 10 passos a norte e, em seguida, 10 passos a leste e aí estará o tesouro”. A quantos passos, em linha reta, está o tesouro da torre de transmissão de energia? (Admita que todos os passos têm o mesmo comprimento e despreze as dimensões da torre de transmissão de energia).
Considere as seguintes matrizes:
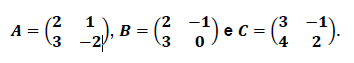
Se 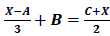 , então a matriz X é tal que a soma dos elementos da diagonal principal é igual a
, então a matriz X é tal que a soma dos elementos da diagonal principal é igual a
Um repórter entrevistando três atrizes perguntou a idade de cada uma. Nenhuma quis revelar a idade, mas uma delas informou que as idades das atrizes mais novas estão entre 20 e 40 anos e, hoje, ambas são expressas por um número primo, fato que se repetirá daqui a 6 anos. Além disso, revelou também que a idade da atriz mais velha, que hoje também é expressa por um número primo maior do que 60, é três unidades a mais do que a soma das idades das atrizes mais novas. Nessas condições, hoje, a soma das idades das três atrizes é igual a
Sobre exponenciais e função exponencial, assinale a alternativa correta.
Os Parâmetros Curriculares Nacionais de Matemática têm como finalidade fornecer elementos para ampliar o debate nacional sobre o ensino dessa área do conhecimento, socializar informações e resultados de pesquisa, levando-os ao conjunto dos professores brasileiros. A respeito dos PCNs-Matemática, assinale a alternativa INCORRETA.
O valor de x para o qual
O domínio da função
Uma fábrica produz dois tipos de peças, A e B. Admitindo que x é a quantidade de peças do tipo A e y é a quantidade de peças do tipo B, produzidas por hora, a relação entre x e y é dada (
Em uma escola, 2/3 dos professores são mulheres e dessas 1/4 têm pós-graduação. A quantidade de professores homens que têm pós-graduação corresponde à metade da quantidade de professores mulheres que têm pós-graduação. Nessas condições, a quantidade de professores (homens e mulheres) que, juntos, têm pós-graduação corresponde a qual porcentagem do total de professores dessa escola?
Sobre números reais, assinale a alternativa INCORRETA.
Uma professora, ao ensinar frações a seus alunos, procedeu ao que segue:
I. Fração é o resultado de duas operações sucessivas sobre o mesmo todo, de natureza contínua ou discreta. A primeira operação divide o todo em n partes e a segunda reúne, em um outro todo, um certo número m de partes, sendo m < n, m > n ou m = n.
II. Para justificar que na divisão de duas frações mantemos a fração do numerador e multiplicamos essa fração pelo inverso da fração do denominador, podemos utilizar a propriedade: “Em toda divisão de frações, se multiplicarmos o numerador e o denominador por um mesmo número (diferente de zero), obteremos uma fração equivalente à fração dada. Nesse caso, o número é o inverso da fração do denominador”.
III. Para justificar que 1/3 > 1/4, podemos proceder como segue: “Primeiro, separamos, por exemplo, 18 tampinhas e as colocamos em 3 pratinhos, contendo 6 tampinhas em cada pratinho. Ao pegarmos um pratinho, estaremos pegando 6 tampinhas, ou seja, 1/3 do todo. Em seguida, pegamos, por exemplo, 16 tampinhas e as colocamos em 4 pratinhos contendo 4 tampinhas em cada pratinho. Ao pegarmos um pratinho, estaremos pegando 4 tampinhas, ou seja, 1/4 do todo. Como 6 tampinhas é maior do que 4 tampinhas, a fração 1/3 é maior do que 1/4”.
IV. Ao se trabalhar com frações quando o todo é de natureza contínua, podemos, matematicamente, obter infinitas frações; se o todo for de natureza discreta, teremos um número finito de frações.
Assinale a alternativa que aponta os procedimentos nos quais a professora NÃO cometeu falha conceitual ou didática.
Davi recebeu um prêmio em dinheiro e decidiu dividir esse prêmio em três partes inversamente proporcionais às idades de seus filhos: 5, 7 e 11 anos. Não quis revelar o montante recebido, mas revelou que a menor parte foi de R$ 7.000,00. Nessas condições, o valor do prêmio recebido por Davi foi de
Um artesão fabrica dois objetos maciços: um tem o formato de uma semiesfera de 20 cm de diâmetro e o outro tem o formato de um cone de raio 5 cm e altura 5 cm. Quantas semiesferas ele precisa fundir para consegui fazer 32 cones, com as especificações mencionadas?
(Admita que não há perda de material durante o processo).
Considerando os conceitos da Geometria Plana e da Geometria Espacial, assinale a alternativa INCORRETA.
Considere a equação (m – 1)x2 –2mx + (m + 2) = 0 na variável x, em que m é um número real e diferente de 1. Nessas condições, analise as assertivas a seguir e assinale a alternativa que aponta a(s) corretas(s).
I. Se m > 2, a equação não possui raízes reais.
II. Existem apenas dois valores reais de m para os quais a equação admite raízes reais.
III. Se m > 2, a equação possui pelo menos uma raiz real.
IV. Para algum m < 2, a equação possui duas raízes reais e distintas cuja soma é zero.

