O tamanho mínimo que a visão humana é capaz de visualizar sem o uso de equipamento auxiliar é equivalente a 100 micrômetros (1 micrômetro =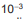 
milímetros). Uma estudante pretende visualizar e analisar hemácias do sangue humano, que medem 0,007 mm de diâmetro. Ela adquiriu um microscópio óptico que tem uma lente ocular que amplia em 10 vezes a imagem do objeto em observação, e um conjunto de lentes objetivas com estas capacidades de ampliação:
• lente I: 2 vezes;
• lente II: 10 vezes;
• lente III: 15 vezes;
• lente IV: 1,1 vez;
• lente V: 1,4 vez.
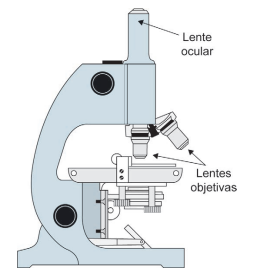
O funcionamento desse microscópio permite o uso da lente ocular sozinha ou a combinação dela com uma de suas lentes objetivas, proporcionando, nesse caso, um aumento de sua capacidade de ampliação final, que é dada pelo produto entre as capacidades de ampliação da ocular e da objetiva.
Essa estudante pretende selecionar a lente objetiva de menor capacidade de ampliação que permita, na combinação com a ocular, visualizar hemácias do sangue humano.
A lente objetiva a ser selecionada pela estudante é a
Um proprietário pretende instalar um sensor de presença para a proteção de seu imóvel. O sensor deverá detectar movimentos de objetos e pessoas numa determinada região plana. A figura ilustra a vista superior da área de cobertura (setor circular em azul) de um sensor
colocado no ponto S. Essa área depende da medida do ângulo α, em grau, e do raio R, em metro.
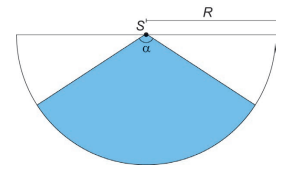
Ao aumentar o ângulo α ou o raio R aumenta-se a área de cobertura do sensor. Entretanto, quanto maior essa área, maior o preço do sensor.
Para esse fim, há cinco tipos de sensores disponíveis no mercado, cada um com as seguintes características:
• tipo I: α = 15° e R = 20 m;
• tipo II: α = 30° e R = 22 m;
• tipo III: α = 40° e R = 12 m;
• tipo IV: α = 60° e R = 16 m;
• tipo V: α = 90° e R = 10 m.
Esse proprietário pretende adquirir um desses sensores que seja capaz de cobrir, no mínimo, uma área de medida 70 m2, com o menor preço possível.
Use 3 como valor aproximado para π.
O proprietário do imóvel deverá adquirir o sensor do tipo
Uma casa de shows terá um evento cujo custo total de produção é de R$ 34 350,00, sendo que comporta 500 pessoas. O preço do ingresso será de R$ 130,00 e, normalmente, 60% das pessoas adquirem meia-entrada, pagando R$ 65,00 pelo ingresso. Além do faturamento proveniente da venda de ingressos, a casa de shows vende, com 60% de lucro, bebidas e petiscos ao público no dia do evento.
Após ter vendido todos os 500 ingressos, constatou-se que a quantidade de meias-entradas vendidas superou em 50% o que estava previsto, impactando o faturamento estimado com a venda de ingressos.
No dia do evento, decidiu-se manter o percentual de 60% de lucro sobre as bebidas e petiscos, pois todo o público que comprou ingresso compareceu ao show. Com isso, espera-se ter lucro de R$ 17 000,00 nesse evento.
Para que se alcance o lucro esperado, o gasto médio por pessoa com bebidas e petiscos, em real, deverá ser de
Uma imobiliária iniciou uma campanha de divulgação para promover a venda de apartamentos que podem ser pagos em 100 parcelas mensais. O valor da primeira delas é fixado no momento da compra, com o pagamento dessa primeira parcela. A partir da segunda parcela, o valor é determinado pela aplicação de um acréscimo percentual fixo ao valor da parcela anterior. Como atrativo, a imobiliária
fará o pagamento de todas as parcelas correspondentes ao mês de aniversário do comprador.
Um cliente, que faz aniversário no mês de maio, decidiu comprar um desses apartamentos por meio do financiamento oferecido pela imobiliária, e pretende escolher o mês mais adequado para realizar essa compra, de modo que o valor total dos pagamentos seja o menor possível.
Qual é o mês que esse cliente deverá escolher para realizar a compra do apartamento?
Uma caneca com água fervendo é retirada de um forno de micro-ondas. A temperatura T, em grau Celsius, da caneca, em função do tempo t, em minuto, pode ser modelada pela função 
representada no gráfico a seguir.
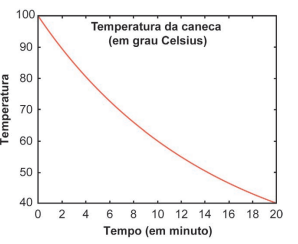
Os valores das constantes a e b são
Em um jogo virtual para celular, um personagem pode percorrer trajetórias retilíneas voando ou se deslocando ao longo de paredes. Considere que o personagem descreve a trajetória ABCDEF, em que os pontos A, D e E estão em um plano paralelo ao que contém os pontos B e C, sendo esses dois planos ortogonais ao plano da base que contém o ponto F, conforme a figura.
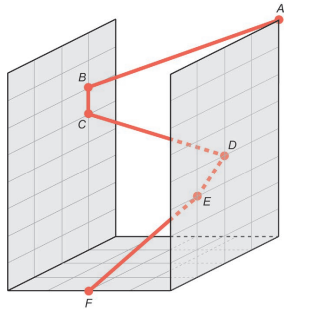
A projeção ortogonal, sobre o plano da base, da trajetória ABCDEF descrita pelo personagem é
Uma empresa de engenharia foi contratada para realizar um serviço no valor de R$ 71250,00. Os sócios da empresa decidiram que 40% desse valor seria destinado ao pagamento de três engenheiros que gerenciaram o serviço. O pagamento para cada um deles será feito de forma diretamente proporcional ao total de horas trabalhadas. O número de dias e o número de horas diárias trabalhadas pelos engenheiros foram, respectivamente:
• engenheiro I: 4 dias, numa jornada de 5 horas e meia por dia;
• engenheiro II: 5 dias, numa jornada de 4 horas por dia;
• engenheiro III: 6 dias, numa jornada de 2 horas e meia por dia.
Qual a maior diferença, em real, entre os valores recebidos por esse serviço entre dois desses engenheiros?
Contratos de vários serviços disponíveis na internet apresentam uma quantidade excessiva de informações. Isso faz com que o tempo necessário para a leitura desses contratos possa ser longo.
O quadro apresenta uma amostra do tempo considerado necessário para a leitura completa do contrato de alguns serviços digitais.
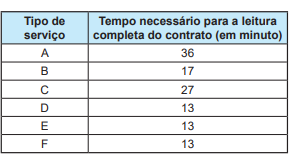
ROMERO, L. Não li e concordo. Superinteressante,
n. 307, ago. 2012 (adaptado).
O tempo médio, em minuto, necessário para a leitura completa de um contrato de serviço dentre os listados no quadro é, com uma casa decimal, aproximadamente,
João e Felipe participaram, na escola, de uma maratona de matemática na qual, durante uma semana, resolveram 200 questões cada. Nessa maratona, a porcentagem P de acertos de cada participante é convertida em um conceito
• insatisfatório: se 0 ≤ P < 50;
• regular: se 50 ≤ P < 60;
• bom: se 60 ≤ P < 75;
• muito bom: se 75 ≤ P < 90;
• excelente: se 90 ≤ P ≤ 100.
João acertou 75% das questões da maratona e Felipe acertou 30% a menos que a quantidade de questões que João acertou.
Os conceitos de João e Felipe foram, respectivamente,
Um tanque, em formato de paralelepípedo reto retângulo, tem em seu interior dois anteparos verticais, fixados na sua base e em duas paredes opostas, sendo perpendiculares a elas, conforme a figura.
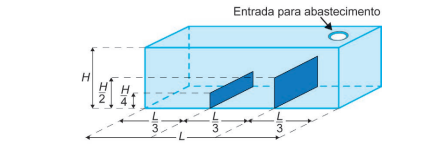
Esses anteparos, de espessuras desprezíveis, estão instalados de maneira a dividir a base do tanque em três retângulos congruentes, tendo suas alturas iguais à metade e a um quarto da altura do tanque. O tanque é abastecido por uma entrada situada no teto, através de um duto que despeja água a uma vazão constante, sendo necessárias 12 horas para finalizar o seu enchimento.
O gráfico que descreve, em cada instante, a maior altura de coluna de água, dentre aquelas que vão sendo formadas ao longo do enchimento do tanque, é
Uma empresa tem 400 funcionários, distribuídos em três setores: administrativo, logística e produção. O gráfico apresenta a distribuição quantitativa desses funcionários, por setor e por faixa etária.
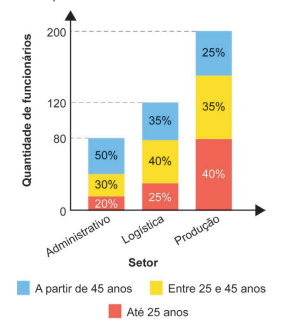
Uma viagem de férias será sorteada entre esses funcionários, de forma que todos terão igual probabilidade de serem sorteados.
A maior probabilidade é que o funcionário sorteado esteja na faixa etária
Uma tubulação despeja sempre o mesmo volume de água por unidade de tempo em uma caixa-d’água, o que significa dizer que a vazão de água nessa tubulação é constante. Na junção dessa tubulação com a caixa-d’água, está instalada uma membrana de filtragem cujo objetivo é filtrar eventuais impurezas presentes na água, combinado a um bom fluxo de água. O fluxo (φ) de água através da superfície da membrana é diretamente proporcional à vazão de água na tubulação, medida em mililitro por segundo, e inversamente proporcional à área da superfície da membrana, medida em centímetro quadrado.
A unidade de medida adequada para descrever o fluxo (φ) de água que atravessa a superfície da membrana é
Uma professora de matemática utiliza em suas aulas uma “máquina caça-números” para verificar os conhecimentos de seus estudantes sobre representações de números racionais. Essa máquina tem um visor dividido em seis compartimentos e, na lateral, uma alavanca. Cada estudante puxa a alavanca e espera que os compartimentos parem de girar. A partir daí, precisa responder para a professora em quais posições se encontram os números que representam a mesma quantidade.
Um estudante puxou a alavanca, aguardou que os compartimentos parassem de girar e observou os números apresentados no visor. A configuração da máquina naquele instante está apresentada na imagem.
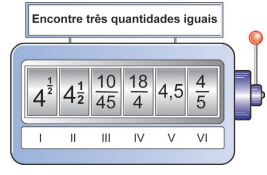
Esse estudante respondeu corretamente à pergunta da professora.
As posições indicadas pelo estudante foram
Uma criança, utilizando um aplicativo, escreveu uma mensagem para enviar a um amigo. Essa mensagem foi escrita seguindo estas etapas:
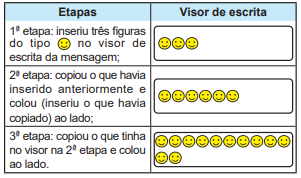
A criança seguiu copiando e colando, em cada etapa, o que tinha no visor na etapa imediatamente anterior, até concluir a 20ª etapa. Em seguida, enviou a mensagem.
Qual foi o total de figuras contidas na mensagem enviada?
A densidade demográfica de uma região é definida como sendo a razão entre o número de habitantes dessa região e sua área, expressa na unidade habitantes por quilômetro quadrado. Uma região R é subdividida em várias outras, sendo uma delas a região Q. A área de Q é igual a três quartos da área de R, e o número de habitantes de Q é igual à metade do número de habitantes de R. As densidades demográficas correspondentes a essas regiões são denotadas por d(Q) e d(R).
A expressão que relaciona d(Q) e d(R) é
