Sejam as funções trigonométricas f(x) = 2 sen 2x e g(x) = sen x cujos gráficos são construídos no mesmo plano cartesiano. Marque a alternativa que corresponde ao número de vezes em que os gráficos das funções f e g se interceptam no intervalo [0,2π[.
Considere os pontos de coordenadas (x,y) associados à matriz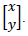 
Na figura representada no plano cartesiano da figura 1 pretende-se fazer uma rotação em torno da origem deixando-a como na figura 2. Para isso deve-se multiplicar uma matriz M pela matriz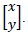 
A matriz M é:
Para a - b ≠ 0 é correto afirmar que:
Considere um número ∝∈Ζ e as funções f(x) = 
e g(x) = log2 x. Sabe-se que a distância entre os pontos
Treze carros de mesmo modelo serão aleatoriamente enfileirados, lado a lado. Quatro deles são azuis, três são pretos, cinco brancos e um vermelho. Cada carro tem uma numeração que também será registrada em um cartão, e estes, colocados em uma mesma urna. Ao se retirar aleatoriamente os cartões, um a um, identifica-se o carro e o estaciona. Qual a probabilidade de que todos os carros de mesma cor fiquem juntos?
No Pisa, avaliação internacional da OCDE, o cenário é difícil para jovens de 15 a 16 anos. Desde 2009, o Brasil não apresenta avanços nesta avaliação. Com o gráfico abaixo vemos a evolução da média do Brasil em Matemática no Pisa. Temos um grande desafio - 46,5% de nossos alunos na rede pública estão abaixo do nível 1 em Matemática.
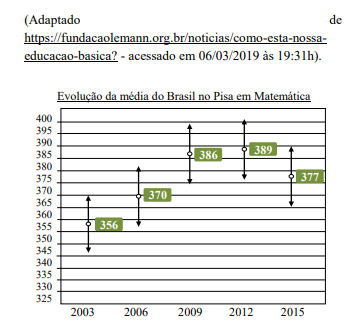
Seja xi a média em Matemática obtida pelo Brasil no Pisa e
Num programa de TV tem um quadro que premia participantes previamente selecionados. O melhor dos prêmios é um carro zero quilômetro. Para ganhar esse prêmio o participante tem que girar três vezes uma roleta com numeração de 1 a 10. Se a soma dos números obtidos nos três giros for menor que 10, o participante leva o prêmio. Ao girar a roleta três vezes, qual a probabilidade de um participante ganhar o carro?
Sejam as funções f(x) e g(x) tais que
- f(x) = ax2 + bx + c com raízes x1 e x2, e
- g(x) = x2 + bx + ac com raízes x'1 e x'2.
É possível garantir para quaisquer
Em um retângulo
Considerando o conjunto ℕ, marque a única proposição falsa:
Dada uma função f , inversível em todo o seu comínio, é certo afimar que o gráfico de sua inversa f -1 é simétrico ao gráfico de f em relação:
A. À bissetriz dos quadrantes ímpares.
B. À bissetriz dos quadrantes pares.
C. Ao eixo das abscissas.
D. Ao eixo das ordenadas.
E. À origem.
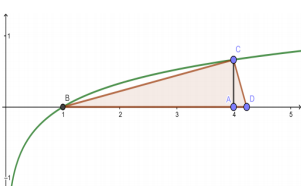
Seja um triângulo retângulo BCD, com ângulo reto em C e altura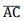 
relativa à hipotenusa BD. Seus vértices B e C são pontos do gráfico de f(x) = log8x cujas abscissas são, respectivamente, 1 e 4. Determine a área do triângulo BCD.
Várias civilizações, de diferentes lugares e diferentes épocas, colaboraram com o desenvolvimento da álgebra. Esse desenvolvimento passou por três estágios quanto à linguagem adotada na resolução de problemas. Nesselmann, em 1842, as diferenciou da seguinte forma:
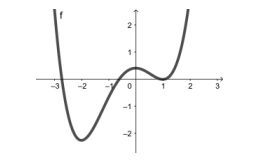
A respeito da função que gera o gráfico abaixo, é possível afirmar que:
Uma espiral foi construída usando uma sequência de semicircunferências cujos raios são os respectivos valores da sequência semicircunferências cujos raios são os respectivos valores da sequência S = (1,5,9,13,17, ... , an). Considerando que seja formada uma circunferência com todo o comprimento da espiral, é certo afirmar que a área do círculo correspondente a essa circunferência é:
