Em uma pequena clínica hospitalar, a receita diária R e a despesa diária D, ambas em R$ mil, são variáveis aleatórias contínuas, tais que:
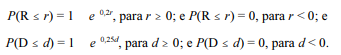
Considerando que a covariância entre as variáveis R e D seja igual a 10, e que
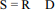seja o saldo diário, julgue o item a seguir.
A correlação linear entre as variáveis aleatórias R e S é igual a 0,5.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e 
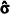representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
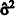é um estimador viciado (ou tendencioso) para a variância populacional, pois 
.
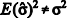X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que e 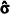representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
O estimador de máxima verossimilhança para a função de densidade da distribuição normal em questão é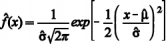 
, para qualquer valor real x.
Considerando que X e Y sejam variáveis aleatórias mutuamente independentes que seguem distribuição normal padrão, julgue o próximo item.
A soma dos quadrados Q = X2 + Y2 segue uma distribuição exponencial com média igual a 2.
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que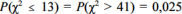 
, em que 
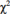representa a distribuição qui-quadrado com 25 de liberdade, e que 
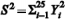, julgue o item a seguir.
[S 2/41;S2/13] representa um intervalo de 95% de confiança para a variância σ2.
Um paciente que compre, mensalmente, determinado medicamento pode optar pelos fornecedores A ou B. Suponha que, em cada mês t(t= 1, 2, 3, ...), essa opção seja feita de acordo com um processo de Markov de primeira ordem: denotada por {Z}, em que, no mês t, Zt = 1, se o paciente optar pelo fornecedor A, ou Zt = 0, se ele optar pelo fornecedor B.
Na matriz
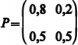, cada entrada Pij, i, j = 0 ou 1 representa a probabilidade de transição do estado i no instante t 1 para o estado j no instante t.
Com base nessas informações, julgue o item a seguir.
Se, nos meses 13 e 14, o paciente tiver optado pelo fornecedor B, então a probabilidade de ele optar novamente pelo fornecedor B no mês 15 é inferior a 0,49.
O toal diário – X – de pessoas recebidas em uma unidade de pronto atendimento (UPA) para atendimento ambulatorial, e o total diário – Y – de pessoas recebidas nessa mesma UPA para atendimento de urgência seguem processos de Poisson homogêneos, com médias, respectivamente, iguais as 20 pacientes/dia e 10 pacientes/dia, e as variáveis aleatórias X e Y são independentes. Sabe-se que, em média, a necessidade de cuidados hospitalares atinge 10% dos pacientes do atendimento ambulatorial e 90% dos pacientes do atendimento de urgência.
A partir dessa situação hipotética, julgue o próximo item, considerando que o registro da necessidade de cuidados hospitalares seja feito no momento em que o paciente chegue à UPA e que H seja a quantidade diária registrada de pacientes com necessidades de cuidados hospitalares.
A quantidade diária H segue uma distribuição de Poisson.
Em determinado hospital, o tempo de espera por atendimento ambulatorial para cada paciente, em minutos, é uma variável aleatória X que segue distribuição normal com média μ e desvio padrão σ. Para o controle estatístico da qualidade de atendimento nesse hospital, registram-se os valores dos tempos X, e os tempos observados são tratados estatisticamente e organizados em forma de gráficos de controle de qualidade denominados "cartas de Shewhart". A tabela seguinte apresenta as médias e as amplitudes observadas em 4 amostras de tamanho n = 5.
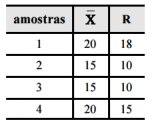
A partir das informações e da tabela precedentes, julgue o item seguinte, considerando que a situação em tela se encontre sob controle e que Φ(3) = 0,9987, em que Φ(z) representa a função de distribuição acumulada da distribuição normal padrão
A amplitude R proporciona estimativas tendenciosas do desvio padrão σ.
Determinado estudo considerou um modelo de regressão linear simples na forma yi = β0 + β1xi + εi, em que yi representa o número de leitos por habitante existente no município i; xi representa um indicador de qualidade de vida referente a esse mesmo município i, para i = 1, ..., n. A componente εi representa um erro aleatório com média 0 e variância σ2. A tabela a seguir mostra a tabela ANOVA resultante do ajuste desse modelo pelo método dos mínimos quadrados ordinários.
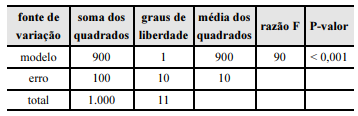
A partir das informações e da tabela apresentadas, julgue o item subsequente.
A correlação linear entre o número de leitos hospitalares por habitante (y) e o indicador de qualidade de vida (x) foi igual a 0,9.
A série temporal da quantidade mensal de pacientes submetidos a determinado procedimento cirúrgico segue um processo na forma Xt = 100 + 0,5Xt 1 + αt 0,5αt 1, em que {αt} representa uma série temporal de ruídos aleatórios com média nula e variância 9.
A respeito desse processo, julgue o item que se segue.
A série temporal {Xt} é estacionária.
Deseja-se estimar o total de carboidratos existentes em um lote de 500.000 g de macarrão integral. Para esse fim, foi retirada uma amostra aleatória simples constituída por 5 pequenas porções desse lote, conforme a tabela seguinte, que mostra a quantidade x amostrada, em gramas, e a quantidade de carboidratos encontrada, y, em gramas.
Com base nas informações e na tabela apresentadas, julgue o item a seguir.
Considerando o estimador de razão, estima-se que existem 250.000 g de carboidratos nesse lote de macarrão integral.
Em relação ao planejamento estratégico hospitalar, julgue o item seguinte.
No planejamento estratégico, a entidade define ou revê a sua missão — situação em que ela pretende estar em um período de tempo definido —, sua visão — propósito de ela existir e seu papel na sociedade — e os seus valores — princípios que delineiam as suas decisões.
Em relação ao planejamento estratégico hospitalar, julgue o item seguinte.
No planejamento estratégico, a entidade, em primeiro lugar, deve definir os indicadores que deseja medir e, a partir deles, definir sua direção estratégica e seus objetivos corporativos.
Julgue o item que se segue, a respeito da estrutura física hospitalar.
Para o armazenamento de cilindros de gases inflamáveis, como o hidrogênio e o acetileno, recomenda-se mantê-los a uma distância mínima de quatro metros daqueles que contenham gases oxidantes, como oxigênio e óxido nitroso, ou utilizar barreiras vedadas e resistentes ao fogo para separar os dois grupos de cilindros.
Acerca das responsabilidades da administração hospitalar, julgue o item subsequente.
Antes de se decidir incorporar um novo equipamento ao estabelecimento de assistência à saúde, deve-se comparar a nova tecnologia, objeto de análise, e aquelas já incorporadas, no que diz respeito à evidência de benefícios, aos custos, à população-alvo, às necessidades de adaptação da infraestrutura na rede de serviços e aos fatores de promoção da equidade.
