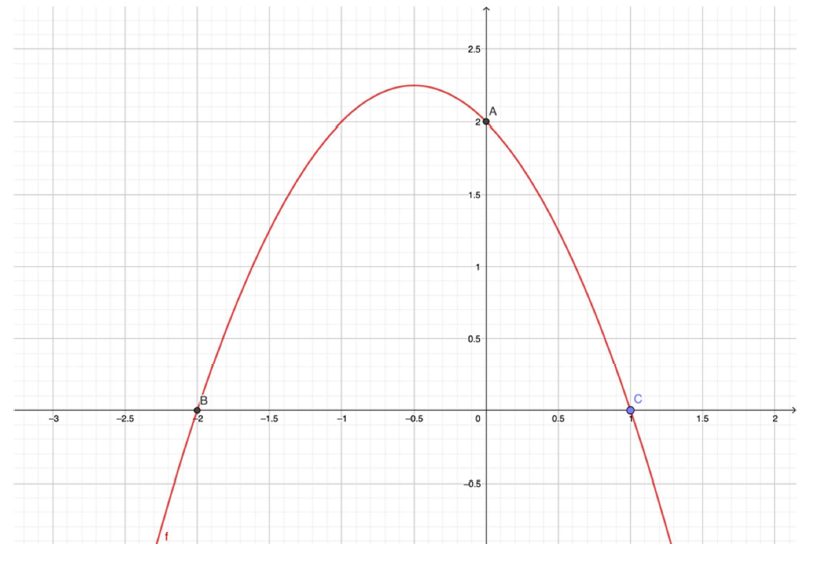
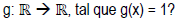Quanto a equações e inequações de 1.º e 2.º graus, julgue o próximo item.
O sistema linear terá sempre solução única, para todo M ℝ.
Julgue o item a seguir, relacionados a problemas aritméticos.
Se, para uma progressão aritmética, a soma dos 2 primeiros termos é 100 e a soma dos 6 primeiros termos é 276, então existirá um n ℕ tal que a soma dos n primeiros termos dessa progressão aritmética será negativa.
A respeito das funções e suas propriedades, julgue o item subsecutivo.
A combinação de funções trigonométricas é uma função periódica de período
Uma pirâmide de base retangular tem volume igual a 36. As arestas da base da pirâmide são então duplicadas e a altura, triplicada.
O volume da nova pirâmide é
A altura de um retângulo é o dobro de sua base e seu perímetro mede 84 cm.
A área desse retângulo em cm2 é
Jorge comprou um celular de R$ 1.200,00. O pagamento foi feito com uma entrada de R$ 600,00, e o restante foi pago ao final de um mês, com juros simples de 1,8%. O valor pago por Jorge, ao final do mês, em reais, foi de:
Considere as duas listas de números a seguir.
Lista 1: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Lista 2: 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15
Sejam D1 e D2 os desvios padrão das Listas 1 e 2, respectivamente.
É correto concluir que
Uma professora, ao ensinar frações a seus alunos, procedeu ao que segue:
I. Fração é o resultado de duas operações sucessivas sobre o mesmo todo, de natureza contínua ou discreta. A primeira operação divide o todo em n partes e a segunda reúne, em um outro todo, um certo número m de partes, sendo m < n, m > n ou m = n.
II. Para justificar que na divisão de duas frações mantemos a fração do numerador e multiplicamos essa fração pelo inverso da fração do denominador, podemos utilizar a propriedade: “Em toda divisão de frações, se multiplicarmos o numerador e o denominador por um mesmo número (diferente de zero), obteremos uma fração equivalente à fração dada. Nesse caso, o número é o inverso da fração do denominador”.
III. Para justificar que 1/3 > 1/4, podemos proceder como segue: “Primeiro, separamos, por exemplo, 18 tampinhas e as colocamos em 3 pratinhos, contendo 6 tampinhas em cada pratinho. Ao pegarmos um pratinho, estaremos pegando 6 tampinhas, ou seja, 1/3 do todo. Em seguida, pegamos, por exemplo, 16 tampinhas e as colocamos em 4 pratinhos contendo 4 tampinhas em cada pratinho. Ao pegarmos um pratinho, estaremos pegando 4 tampinhas, ou seja, 1/4 do todo. Como 6 tampinhas é maior do que 4 tampinhas, a fração 1/3 é maior do que 1/4”.
IV. Ao se trabalhar com frações quando o todo é de natureza contínua, podemos, matematicamente, obter infinitas frações; se o todo for de natureza discreta, teremos um número finito de frações.
Assinale a alternativa que aponta os procedimentos nos quais a professora NÃO cometeu falha conceitual ou didática.
Davi recebeu um prêmio em dinheiro e decidiu dividir esse prêmio em três partes inversamente proporcionais às idades de seus filhos: 5, 7 e 11 anos. Não quis revelar o montante recebido, mas revelou que a menor parte foi de R$ 7.000,00. Nessas condições, o valor do prêmio recebido por Davi foi de
Um artesão fabrica dois objetos maciços: um tem o formato de uma semiesfera de 20 cm de diâmetro e o outro tem o formato de um cone de raio 5 cm e altura 5 cm. Quantas semiesferas ele precisa fundir para consegui fazer 32 cones, com as especificações mencionadas?
(Admita que não há perda de material durante o processo).
Considerando os conceitos da Geometria Plana e da Geometria Espacial, assinale a alternativa INCORRETA.
Uma aplicação de R$ 1.000.000,00, no regime de capitalização contínua, produz R$ 1.491.806,73 de montante após o período de 5 anos. A taxa instantânea dessa aplicação é de
Três números de 4 dígitos são escritos em 3 pedaços de papel, observou-se então que a soma total dos números era de 17.215.
Porém, após algum tempo, 3 dígitos foram rasurados e os 3 papéis ficaram assim:
A soma dos três dígitos rasurados é

Determine o valor de
Seja a representação gráfica da função quadrática definida por 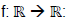
Quais os pontos intersectam os gráficos de f e g, definida pela função