Sabe-se que a média dos dados da planilha A é igual a Z e que a média dos valores da planilha B é igual a Y. Assim, ao unificar os dados de ambas as planilhas, pode-se obter a média geral de todos esses valores, que será igual a Y + Z / 2.
As sentenças “Não se faz mais carro como antigamente” e “Precisa-se de trabalhador capacitado”, com os termos destacados passados para o plural, ficariam, sem prejuízo à correção gramatical, “Não se fazem mais carros como antigamente” e “Precisa-se de trabalhadores capacitados”.
Uma pista de pouso de avião cuja medida inicial era de 344 metros foi ampliada, passando a medir 502 metros. Assim, é correto afirmar que ocorreu um aumento de 53,93% na pista.
Uma fábrica vende mensalmente 200 malas a R$ 300,00 cada. O departamento de vendas trabalha com a hipótese de que cada aumento de R$ 10,00 no preço de cada mala implica a venda mensal de 20 malas a menos. Por exemplo, em um mês em que cada mala foi vendida por R$ 320,00, foram vendidas 160 malas. Suponha que a hipótese esteja correta e que, em um determinado mês, cada mala foi vendida por (300 + 10x) reais, sendo x o número inteiro de aumentos de R$ 10,00, tal que 0 < x < 10.
Nesse mês, com a venda dessas malas, o valor y, em reais, arrecadado, em função de x, é dado por
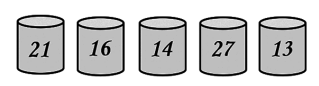
Em cada uma da slatas da Figura acima há apenas lápis e borrachas. O número escrito em cada uma dessas latas indica a quantidade total desses objetos nela contidos. Uma dessas latas foi retidada e, considerando-se apenas as quatro latas restantes, o número total de lápis passou a ser o triplo do número total de borrachas.
Considerando-se apenas as quatro latas restantes, o número total de lápis existente nelas é igual a
As irmãs N, T e S apostaram uma corrida. Elas têm uma peculiaridade: N nunca mente; T às vezes mente; S sempre mente.
• Quem ficou em 1° lugar disse: “S ficou em 2° lugar”.
• Quem ficou em 2° lugar disse: “Eu sou T”.
• Quem ficou em 3° lugar disse: “N ficou em 2° lugar”.
Nessa corrida, tem-se como 1° lugar, 2° lugar e 3° lugar, respectivamente,
Em um pacote, há algumas cédulas de R$ 10,00, algumas de R$ 20,00, algumas de R$ 50,00 e nada mais. Ao todo, são 68 cédulas, que totalizam R$ 1.380,00. Sabe-se que, contando só as cédulas de R$ 50,00, obtém-se R$ 550,00, e contando só as cédulas de
R$ 20,00, obtém-se R$ 520,00.
Nesse pacote, o número de cédulas de R$ 10,00 é igual a
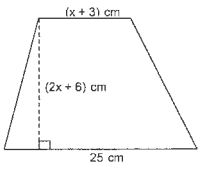
Na imagem abaixo está representado um trapézio que possui 774 cm2 de área, mas pá-l'a' a identificação de algumas de suas medidas é necessário a identificação do valor atribuido a variável x, presente na forma algébrica de algumas delas. Com base nessas informações, podemos concluir que a medi_da_dél_altura desse trapézio é igual a:
As figuras a seguir representam os 4 primeiros termos da sequência de números pentagonais: (1, 5, 12, 22, ...)
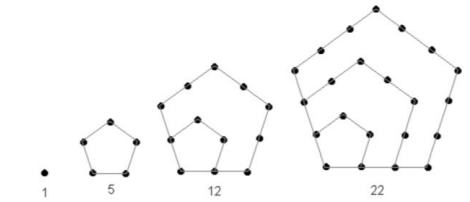
O número que ocupa a 7ª posição nessa sequência é
Os preços de um determinado medicamento em quatro diferentes farmácias são, respectivamente: R$ 32,00, R$ 19,10, R$ 41,80, R$ 8,20. Assim, é correto afirmar que o preço médio desse medicamento é superior a R$ 25,00.
Uma empreiteira está construindo um parque aquático e precisa determinar as dimensões de uma piscina em forma de retângulo. A área total disponível para a piscina é de 600 metros quadrados. A empresa quer maximizar a área da piscina, considerando que um dos lados será 10 metros maior que o outro. Assim, é correto afirmar que o maior lado dessa piscina é igual a 40 m.
Um estudante da rede municipal de ensino se deparou com o seguinte problema de estatística: em um grupo de n números aleatórios, a média aritmética é igual a 290. Ao retirar o número 100 desse grupo, a média aumenta para 300. O estudante fez seus cálculos e encontrou o valor de n igual a 10. Com base nisso, podemos afirmar que a resposta do estudante está correta.
Considere que 344 picolés foram vendidos a R$ 12,98, cada. Sobre o valor total arrecadado com essas vendas, foi cobrado um imposto de 3,21%. Assim, é correto afirmar que o valor total do imposto recolhido é superior a R$ 188,00.
Em uma pequena cidade há três agências de um banco, nomeadas A1, A2 e A3. Técnicos desse banco estão analisando um mapa para escolher o local para abrir uma quarta agência. A Figura a seguir é um esboço desse mapa, que contém também as seguintes informações:
• Para ir de A1 para A2, passando por A3, percorrem-se 7,8 km;
• Para ir de A3 para A1, passando por A2, percorrem-se 9,9 km;
• Para ir de A2 para A3, passando por A1, percorrem-se 11,3 km.
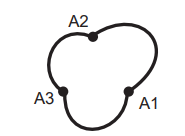
Uma pessoa decidiu ir de A1 para A3, sem passar por A2, depois ir de A3 para A2, sem passar por A1 e, finalmente, ir de A2 para A1, sem passar por A3.
Com base na Figura e nas informações do mapa, essa pessoa percorreu, ao todo, uma distância, em km, igual a
Uma empresa estava patrocinando um evento musical e resolveu presentear alguns de seus melhores clientes com ingressos para o evento. Para cada um dos 30 clientes solteiros, foi enviado um envelope com apenas um ingresso, e, para cada um dos 40 clientes casados, foi enviado um envelope com dois ingressos.
Antes de serem enviados por correio, o conjunto de envelopes com dois ingressos foi pesado, dando uma massa total de 5720g, ao passo que a pesagem do conjunto de envelopes com apenas um ingresso indicou uma massa total de 3090g.
Sabendo-se que os cônjuges dos clientes não eram clientes da empresa e que os envelopes, assim como os ingressos, eram idênticos, qual é a massa, em gramas, de cada ingresso?

