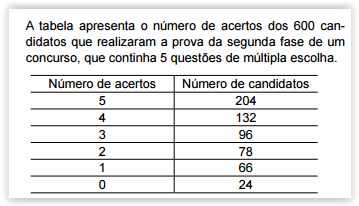
Analisando-se as informações apresentadas na tabela, é correto afirmar que
Alberto, Bruno e Carla foram almoçar em um restaurante e, no final do almoço, cada um pagou o que consumiu. Sabendo-se que, sem a taxa de serviço de 10% sobre o consumo total, Alberto e Bruno consumiram, juntos, R$ 150,00, Bruno e Carla consumiram, juntos, R$ 114,00, e Alberto e Carla consumiram, juntos, R$ 144,00, é correto afirmar que a taxa de serviço de 10% sobre o consumo dessas três pessoas foi
Sabe-se que 16 caixas K, todas iguais, ou 40 caixas Q, todas também iguais, preenchem totalmente certo compartimento, inicialmente vazio. Também é possível preencher totalmente esse mesmo compartimento completamente vazio utilizando 4 caixas K mais certa quantidade de caixas Q. Nessas condições, é correto afirmar que o número de caixas Q utilizadas será igual a
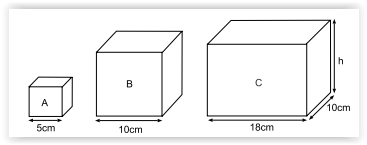
As figuras seguintes mostram os blocos de madeira A, B e C, sendo A e B de formato cúbico e C com formato de paralelepípedo reto retângulo, cujos respectivos volumes, em cm3, são representados por VA, VB e VC.
Se 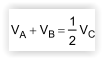
A estimativa para a safra nacional, em 2017, de cereais, leguminosas e oleaginosas é de 230 milhões de toneladas. Sabe-se que a safra de 2016 foi de 184 milhões de toneladas. Se a previsão se concretizar, então, é CORRETO afirmar que, em relação a 2016, o aumento da produção será de
Em 2016, o orçamento de determinada prefeitura era de R$ 3.000.000,00, dos quais R$ 30.000,00 foram destinados à manutenção de uma horta municipal. Em 2017, a mesma prefeitura estima que seu orçamento será de R$ 3.400.000,00. Se a prefeitura mantiver a proporção de recursos para a manutenção de horta, é CORRETO afirmar que em 2017 serão destinados
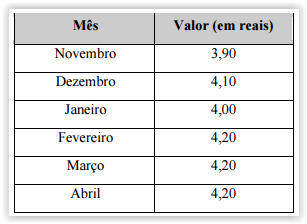
O quadro abaixo apresenta o valor comercializado, por uma empresa, por um produto nos últimos 6 meses. Com base nas informações abaixo, é CORRETO afirmar que o valor médio, nos 6 meses, desse produto foi
Uma corda de 7 metros e 20 centímetros de comprimento foi dividida em três partes iguais. O comprimento de cada parte é:
João recebeu 32 relatórios verdes e 40 relatórios vermelhos. Ele deve colocar esses relatórios em envelopes da seguinte forma:
• Todos os envelopes devem conter a mesma quantidade de relatórios.
• Nenhum envelope pode misturar relatórios de cores diferentes.
Cumprindo essas exigências, o menor número de envelopes que ele precisará utilizar é:
Para o jantar comemorativo do aniversário de certa empresa, a equipe do restaurante preparou 18 mesas com 6 lugares cada uma e, na hora do jantar, 110 pessoas compareceram. É correto afirmar que:
Observe a tabela que mostra as contas que Mariana paga mensalmente utilizando o débito automático em sua conta bancária.
No dia 8 de fevereiro de 2017, ela foi ao banco e verificou que o saldo de sua conta corrente estava negativo em R$ 358,00. Quanto Mariana teve que depositar para que no dia 12 de fevereiro tivesse um saldo positivo de R$ 150,00?
Fábio possui 48 figurinhas e deu 1/4 delas para Artur, 1/8 para Bianca e 5/12 para Carlos. Com quantas figurinhas Fábio ficou?
Seja a expressão 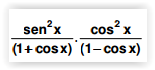
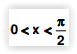
Um aparelho de televisão que custa R$1600,00 estava sendo vendido, numa liquidação, com um desconto de 40%. Marta queria comprar essa televisão, porém não tinha condições de pagar à vista, e o vendedor propôs que ela desse um cheque para 15 dias, pagando 10% de juros sobre o valor da venda na liquidação. Ela aceitou e pagou pela televisão o valor de:
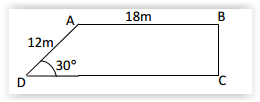
Fábio precisa comprar arame para cercar um terreno no formato a seguir, retângulo em B e C. Considerando que ele dará duas voltas com o arame no terreno e que não terá perdas, quantos metros ele irá gastar? (considere √3 =1,7; sen30º=0,5; cos30º=0,85; tg30º=0,57).