Considere a seguinte sentença quantificada: (∀x) (x + 3 < 5 ∧ x + 7 ≥ 1). Uma negação para a sentença apresentada é:
Um trapézio inscrito em uma circunferência tem um dos ângulos internos com medida igual a 116°. Traçando-se uma das diagonais desse trapézio, toma-se, dos dois triângulos formados, o de maior área. Do triângulo tomado, é correto afirmar que a soma das medidas de dois de seus ângulos internos, que não são ângulos internos do trapézio, é igual a
Ao se inscrever em uma plataforma virtual de xadrez pela primeira vez, um jogador recebe 1.000 pontos. Para cada partida vencida, o jogador ganha 5 pontos, para cada derrota, perde 9 pontos e, para cada empate, ganha 1 ponto.
Com base nessa situação hipotética, julgue o item
Para se compensar os pontos perdidos em 15 derrotas, é necessário vencer 27 partidas.
O Cap R. Gomes é um autêntico “canga”, isto é, um militar que não apenas coopera com os membros de sua equipe, mas estimula superiores, pares e subordinados ao bom cumprimento das missões. Em particular, ele incentiva um grupo de militares a melhorar o desempenho na corrida. Para tal, criou um programa de treinamento em que é preciso correr exatamente 576 Km no total, começando com 26 Km na primeira semana e, a partir da segunda, acrescentando exatos 4 Km a cada semana, ou seja, cada integrante do grupo deve correr exatamente 26 Km na 1a semana, 30 Km na 2a semana, 34 Km na 3a semana e assim sucessivamente. Após quantas semanas a meta de 576 Km será atingida?
O produto (log3 12)⋅[log4(10log107)]⋅[log12(log11114)]⋅(log7 81) é igual a
Em certa cidade, o número de furtos de automóveis em maio de 2020 foi 40% menor do que em janeiro de 2020. De maio de 2020 para janeiro de 2021, houve um aumento de 45% no número de furtos de automóveis.
Nessa cidade, de janeiro de 2020 para janeiro de 2021, com relação ao número de furtos de automóveis, houve
Para abastecer os carros da corporação, há um tanque cilíndrico de combustível, com 2 m de diâmetro e 1,5 m de altura.
A capacidade desse tanque é de, aproximadamente,
Ao efetuarmos corretamente a divisão do número 444 em partes inversamente proporcionais a 4, 5 e 6, encontraremos, respectivamente, A, B e C. Nessas condições é correto afirmar que o valor de C é
Apliquei certa quantia a juros de 5% a.a. No fim de 2 anos e 4 meses, saquei um total de R$ 134.000,00. Qual foi a quantia inicial aplicada?
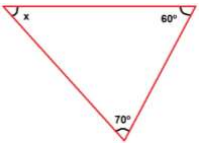
Determine o valor de x na figura a seguir.
Leia a notícia veiculada em um jornal digital.

(www.nexojornal.com.br)
Uma frase que substitui corretamente o dado apresentado na reportagem está indicada em:
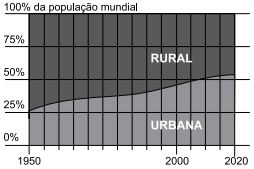
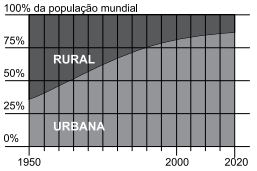
Os gráficos a seguir apresentam a distribuição da população urbana e rural no mundo e no Brasil.
Proporção das populações rural e Urbana no mundo ENTRE 1950 E 2020
Proporção das populações rural e Urbana no Brasil ENTRE 1950 E 2020
 (https://www.nexojornal.com.br. Adaptado)
(https://www.nexojornal.com.br. Adaptado)
Dado que as marcações verticais relacionadas aos anos de referência estão igualmente espaçadas, ao analisar os dados apresentados, tem-se que a maioria dos habitantes do mundo passaram a viver em áreas urbanas entre os anos de_________________, enquanto que, no Brasil, isso ocorreu pouco mais de_______________ anos antes.
Os termos que completam, correta e respectivamente, a frase anterior são:
Estudos feitos em 2018 pelo Instituto Trata Brasil, a partir de dados do Sistema Nacional de Informações sobre Saneamento (Snis), mostrou que cerca de 38% da água potável que passa por sistemas de distribuição no Brasil é desperdiçada em vazamentos durante o processo de produção, tratamento e distribuição. Também entram nessa conta desvios ilegais e furtos de água. Esse volume de água equivale a 7 mil piscinas olímpicas de água potável jogadas fora todos os dias.
Considerando que piscinas olímpicas precisam ter um comprimento de 50 metros, uma largura de 25 metros e profundidade mínima de 2 metros, o volume de água potável desperdiçada diariamente nos sistemas de distribuição no Brasil, segundo o estudo citado anteriormente, é de, no mínimo,
Em um grupo de 218 soldados, 147 são do sexo masculino e 71 do sexo feminino. Para um treinamento, esses 218 soldados são agrupados, aleatoriamente, formando 109 pares de soldados. Sabe-se que, exatamente, 21 pares têm dois soldados do sexo feminino. O número de pares de soldados que têm dois soldados do sexo masculino é
Um retângulo tem um de seus lados aumentado em 2/5 de seu valor e o outro lado diminuído de 1/4 de seu valor. Conclui-se que a área desse retângulo, em relação à área inicial,

