A probabilidade de sair soma 7 no lançamento de dois dados é:
Foi distribuído um bônus de R$ 15 000,00 entre os três melhores funcionários de uma empresa. Se um deles recebeu 20% desse valor, o outro recebeu 45%, o terceiro recebeu, em reais:
A metade de 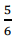 é:
é:
O número de Euler, nome dado em homenagem ao matemático suíço Leonhard Euler, é um número irracional denotado por e, cuja representação decimal tem seus 4 primeiros algarismos dados por 2,718. Esse número é a base dos logaritmos naturais, cuja função f(x) = lnx = logex tem inúmeras aplicações científicas.
A respeito desse assunto, julgue o item a seguir.
A função exponencial g(x) = ex , função inversa de ln x, é uma função crescente.
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
A inversa de
f(x) é expressa por 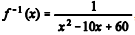
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.
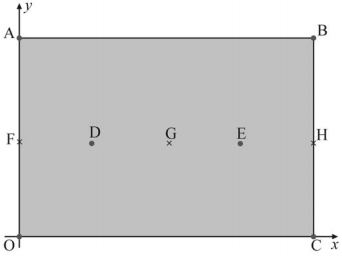
A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
A distância de O a D é superior a 3 × 102 m
A figura seguinte mostra, em um sistema de coordenadas cartesianas ortogonais xOy, em que a unidade de medida é o metro, uma região retangular OABC. O lado OA mede 600 m e o lado OC mede 800 m.

A figura mostra também os pontos F = ponto médio de OA, H = ponto médio de CB, G = centro do retângulo OABC, D = ponto médio de FG, e E = ponto médio de GH. Nos pontos O, A, B, C, D e E foram instalados pontos de acesso à Internet — wi-fi. Nessa configuração, o usuário consegue se conectar à Internet desde que o seu smartphone esteja a 200 m ou menos de qualquer desses pontos de acesso.
Com base nessas informações e na figura apresentada, julgue o próximo item.
Na parte externa ao retângulo OABC, o acesso à Internet a partir dos referidos pontos de acesso se restringe a uma região em que a área é inferior a 384.000 m2.
Com relação a uma sequência numérica a 1, a2, …, an, julgue o item subsequente.
Se a sequência for uma sequência de Fibonacci, em que a1 = 4 e a2 = 9, então a6 = 57.
Julgue o item que se segue, relativo a matrizes e sistemas lineares.
Se P for uma matriz simétrica, então P será inversível.
Acerca de probabilidade e estatística, julgue o próximo item.
Situação hipotética: A média aritmética dos pesos dos 60 alunos de uma sala de aulas é igual a 51,8 kg. Nessa sala, a média aritmética do peso dos meninos é de 62 kg e das meninas, 45 kg. Assertiva: Nesse caso, essa sala de aulas tem 24 meninos e 36 meninas.
Acerca de probabilidade e estatística, julgue o próximo item.
Considere que de uma urna com 10 bolas numeradas de 1 a 10, uma pessoa deva retirar, aleatoriamente, duas bolas ao mesmo tempo. Nesse caso, a probabilidade de que seja 12 a soma dos números das bolas retiradas é superior a 9%.
Com relação a matemática financeira, o item a seguir apresenta uma situação hipotética seguida de uma assertiva a ser julgada.
Para liquidar o estoque de determinado produto, o lojista ofereceu um desconto de 10% no preço de venda. Passados alguns dias, para o estoque remanescente, o lojista concedeu novo desconto, agora de 20% sobre o preço já com primeiro desconto. Nessa situação, o valor do desconto que é equivalente a um único desconto aplicado sobre o preço do produto é igual a 28%.
A respeito de história da matemática, julgue o item subsequente.
A sequência de Fibonacci 1, 1, 2, 3, 5, 8, 13, …,
fn - 1, fn, … foi apresentada no livro Liber Abaci, escrito por Leonardo de Pisa, como solução para um problema sobre a população de coelhos. Essa sequência, desde então, é vastamente estudada por possuir diversas propriedades interessantes, como, por exemplo: a sequência das razões 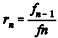
Leia a informação a seguir.

De acordo com estas informações, a razão entre o número de domicílios em 2004 e o número de domicílios em 2012 era, aproximadamente, de
Suponha que um caixa automático de um banco disponibilize para saque uma quantidade suficiente das cédulas da figura abaixo:

Uma retirada de R$ 1.000,00 será feita neste caixa, de modo que nela exista pelo menos uma cédula de cada valor. Se M é o maior e N o menor número de cédulas possíveis de haver nesse saque, então M + N é igual a

