Uma empresa de refrigerantes, que funciona sem
interrupções, produz um volume constante de 1 800 000 cm3
de líquido por dia. A máquina de encher garrafas apresentou
um defeito durante 24 horas. O inspetor de produção
percebeu que o líquido chegou apenas à altura de 12 cm
dos 20 cm previstos em cada garrafa. A parte inferior da
garrafa em que foi depositado o líquido tem forma cilíndrica
com raio da base de 3 cm. Por questões de higiene, o líquido
já engarrafado não será reutilizado.
Utilizando π = ≅3, no período em que a máquina
apresentou defeito, aproximadamente quantas garrafas
foram utilizadas?
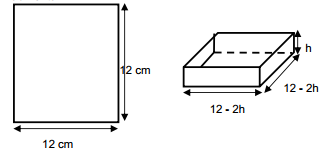
Muitas indústrias têm procurado modificar as embalagens
de seus produtos de forma a economizar material, mas
mantendo o mesmo volume. Considere que se tenha uma
folha de papelão quadrada e se deseje encontrar a
melhor altura (h) para fazer uma caixa sem tampa,
cortando–se os quatro cantos da folha. As exigências são
que as dimensões da caixa sejam números inteiros e que
o volume seja o maior possível. No modelo apresentado
na figura seguinte, a folha tem 12 cm de lado e, nesse
caso, a caixa de maior volume terá altura 2 cm. Para
encontrar esse número, é calculado o volume em função
da altura e prossegue–se atribuindo valores a h e
calculando o volume, enquanto o valor do volume
aumentar.
Se a folha quadrada tiver 20 cm de lado, qual deve ser a
medida do lado do quadrado a ser cortado em cada um
dos cantos, de modo a obter uma caixa sem tampa cujas
dimensões sejam números inteiros e cujo volume seja o
maior possível?

