De acordo com o texto CB1A5-I, se, para cada j = 0, 1, 2, ..., nj indicar a quantidade de municípios cearenses que celebraram, pelo menos, j convênios com o governo estadual, então n1 será igual a
Observe a sequência infinita de figuras formada por quadradinhos.
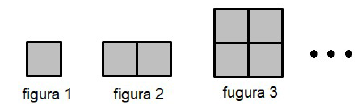
Quantos quadradinhos terá a figura 8?
Sejam P1, P2 e C duas premissas e a conclusão, respectivamente, julgue o item acerca da lógica da argumentação e dos diagramas lógicos.
P1: Nem estudou, nem passou;
P2: Estudou ou passou;
C: Estudou se, e somente se, passou.
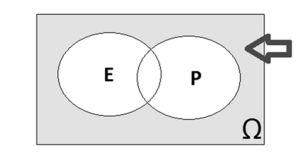
Considerando‐se que E seja o conjunto das pessoas que estudaram e P, o conjunto das pessoas que passaram, a premissa P1 está corretamente representada pela parte assinalada no diagrama lógico abaixo.
Lista de símbolos:
⇒ Condicional
⇔ Bicondicional
∧ Conector “e”
∨ Conector “ou” Conector “ou” exclusivo
Conector “ou” exclusivo
¬ Negação da proposição
Considere as seguintes proposições:
- Todo morador de Vila Lângaro gosta de lógica.
- Todas as pessoas estudiosas gostam de lógica.
- Antônio gosta de lógica.
A partir das proposições apresentadas, pode-se concluir que:
Assinale a opção que apresenta a proposição lógica que é equivalente à seguinte proposição: “Se Carlos foi aprovado no concurso do TJ/PR, então Carlos possui o ensino médio completo.”
Considere as seguintes sentenças.
I. A ouvidoria da justiça recebe críticas e reclamações relacionadas ao Poder Judiciário do estado.
II. Nenhuma mulher exerceu a presidência do Brasil até o ano 2018.
III. Onde serão alocados os candidatos aprovados no concurso para técnico judiciário do TJ/PR?
Assinale a opção correta.
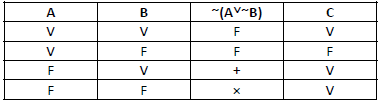
Considerando que a tabela‐verdade acima trate das proposições lógicas A, B e C e de seus valores de verdadeiro (V) e falso (F), que a notação ~A indique a negação da proposição A e que os símbolos + e × estejam, na tabela, no lugar de valores V ou F, julgue o item
Uma possibilidade correta é C = ~A˅B
Se um retângulo tem as medidas de seus quatro lados iguais, então ele é chamado de quadrado. A alternativa que contém uma negação lógica da afirmação anterior é:
São frequentes os episódios em que Pedro ouve o barulho de algum objeto quebrando em seu apartamento e, ao chegar ao local do acidente, encontra seus três cachorros, Totó, Milu e Brutus, em volta do objeto quebrado. Toda vez que isso ocorre, Pedro pergunta para os cachorros em tom firme, apontando para o objeto: Quem foi que quebrou isso? Ele notou que cada cachorro sempre age de uma forma específica, dependendo se foi ou não o responsável pelo acidente e, caso não tenha sido o responsável, se testemunhou ou não o acontecimento.
A tabela a seguir descreve o comportamento de cada cachorro ao ouvir a pergunta feita pelo dono:
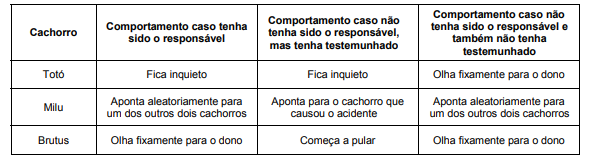
Em um desses episódios, Pedro chega ao local do acidente e pergunta Quem foi que quebrou isso?, observando as seguintes reações:
− Totó olha fixamente para o dono;
− Milu aponta para Totó;
− Brutus olha fixamente para o dono.
Sabendo que o acidente foi causado por apenas um dos cachorros, Pedro pode concluir que
Uma senha foi formada com três algarismos distintos, que foram escolhidos dentre os números inteiros de 1 a 6 e colocados em ordem crescente. Sabe-se que a soma do primeiro com o terceiro algarismo é igual a 7. Nessas condições, se o segundo algarismo da senha for
Em um escritório de contabilidade com 320 funcionários, 184 trabalham no departamento fiscal e 196 trabalham no departamento pessoal. Se, nesse escritório, não há outro departamento senão fiscal e pessoal, então o número de funcionários que se dedicam a apenas um departamento é
Em um curso universitário, são admitidos anualmente 225 novos alunos. No primeiro ano do curso, os alunos ingressantes são divididos em três turmas (A, B e C) considerando seu desempenho no exame vestibular. Na tabela, que mostra como ocorre essa divisão, os números ordinais correspondem à classificação do aluno ingressante no exame vestibular.
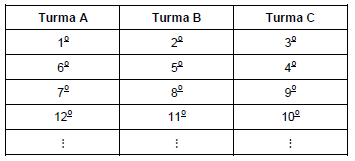
Assim, o primeiro colocado é alocado na turma A, o segundo na B, o terceiro e o quarto na C, e assim sucessivamente, como indicado na tabela. Viviane e Mateus foram aprovados nesse exame vestibular na 122a e na 201a colocações, respectivamente. Dessa forma,
A negação lógica da sentença " se estou de dieta, então fecho a boca" é:
Em uma urna há 3 bolas vermelhas, 5 bolas verdes, 4 bolas brancas e 6 bolas pretas. Retiram-se, aleatoriamente, N bolas da urna.
O valor mínimo de N, para que possamos garantir que entre as N bolas retiradas haja pelo menos duas bolas vermelhas, é
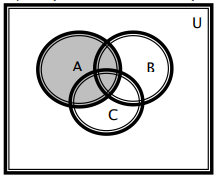
Indique simbolicamente a parte pintada.