Um semáforo é composto por três círculos de luzes coloridas: vermelho, amarelo e verde. Do funcionamento desse semáforo, o sinal vermelho representa 40% do tempo, o sinal verde representa 50% do tempo e o sinal amarelo corresponde a 10% do tempo. O semáforo funciona de modo ininterrupto e não é possível que ele indique mais de um sinal ao mesmo tempo.
Caso um veículo passe 10 vezes por esse semáforo, de forma aleatória, a probabilidade de o veículo se deparar, exatamente, com 4 sinais vermelhos, 5 sinais verdes e 1 sinal amarelo é igual a
Leonor tem uma caixa com 600 botões. Nessa caixa, 2/5 dos botões são brancos e 150 botões são amarelos. Dos restantes, 1/3 são vermelhos e 2/3 são azuis. Leonor vendeu 5% dos botões brancos, 10% dos amarelos e 20% dos vermelhos. Após a venda, o número de botões que restou na caixa foi
As festas juninas são festas tradicionais que ocorrem em todo o país e possuem, além de muita comida e dança, brincadeiras e competições. Por isso, são ambientes excelentes para problemas de contagem e probabilidade e para estudos de fenômenos aleatórios. Com relação a esse tema, julgue o item que se segue.
Situação hipotética: Em determinada festa junina, as primeiras 50 pessoas que chegaram ao local receberam números de 1 a 50 para participarem de um sorteio. Na horade sortear o número vencedor, os participantes foram reunidos e verificou-se que as pessoas que estavam com os números 14 e 27 já haviam ido embora. Sabendo desse fato, a organização excluiu esses dois números do sorteio. Assertiva: Nesse caso, a probabilidade de ter sido sorteado um número que não esteja no conjunto {n∈ ℕ ∶ 15 ≤ n ≤ 26} é inferior a 75%.
As festas juninas são festas tradicionais que ocorrem em todo o país e possuem, além de muita comida e dança, brincadeiras e competições. Por isso, são ambientes excelentes para problemas de contagem e probabilidade e para estudos de fenômenos aleatórios. Com relação a esse tema, julgue o item que se segue.
Situação hipotética: Em uma brincadeira de determinada festa junina, os jogadores devem tirar de uma urna duas bolas em sequência e sem reposição. A urna contém 10 bolas, numeradas de 1 a 10. Para ganhar o jogo, os participantes da brincadeira devem tirar duas bolas cujos números mostrados possuam diferença, em módulo, igual a 1. Assertiva: Nessa situação, a probabilidade de ganhar o jogo é de 20%.
Em uma fila com 12 cadeiras, três delas foram ocupadas aleatoriamente. A cadeira em que Valter deverá se sentar será sorteada entre as cadeiras que estão vazias.
A probabilidade de que Valter não se sente ao lado de nenhuma pessoa já sentada é, no mínimo:
Em uma feira de ciências, cinco crianças, designadas pelas letras A, B, C, D e E, participarão de um experimento no qual um robô distribuirá três tipos de bala: de morango, de laranja ou de hortelã. A cada nova rodada, somente uma bala será dada pelo robô a cada criança, partindo-se da criança A até a criança E, em ordem alfabética, conforme ilustrado na figura a seguir.
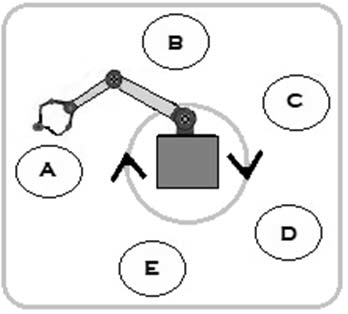
A distribuição das balas seguirá a seguinte rotina, a qual será obedecida também quando se passar de uma rodada para outra: se uma criança receber uma bala de morango, a criança seguinte receberá uma bala de laranja; se uma criança receber uma bala de laranja, a criança seguinte receberá uma bala de hortelã; se uma criança receber uma bala de hortelã, a criança seguinte receberá uma bala de morango.
A partir dessa situação hipotética, julgue os itens seguintes, considerando que a criança A receberá uma bala de morango na primeira rodada.
A probabilidade de duas crianças receberem uma bala de laranja na rodada 42 é inferior a 0,2.
A probabilidade de um jogador acertar determinado alvo em cada rodada de um jogo é igual a 0,6. Na tabela abaixo, por exemplo, em determinada partida, esse jogador acertou o alvo pela primeira vez na quarta rodada.

Caso esse mesmo jogador inicie outra partida, considerando-se que haja independência mútua entre duas rodadas, a probabilidade de ele acertar o alvo, pela primeira vez, na terceira rodada é igual a
As festas juninas são festas tradicionais que ocorrem em todo o país e possuem, além de muita comida e dança, brincadeiras e competições. Por isso, são ambientes excelentes para problemas de contagem e probabilidade e para estudos de fenômenos aleatórios. Com relação a esse tema, julgue o item que se segue.
Situação hipotética: Para determinada apresentação de dança de quadrilha, quatro homens e quatro mulheres devem ficar em fila, de modo que a primeira e a última pessoa da fila sejam mulheres. Assertiva: Nesse caso, há 8.640 formas distintas de organizar essa fila.
O soldado Garcia vai liderar uma equipe de 3 soldados (ele incluído) para uma missão. Os outros 2 soldados da equipe serão sorteados aleatoriamente de um grupo de 6 soldados, sendo que um dos 6 é o soldado Ryan, amigo do soldado Garcia.
A probabilidade de o soldado Ryan ser um dos 2 sorteados é
Em uma feira de ciências, cinco crianças, designadas pelas letras A, B, C, D e E, participarão de um experimento no qual um robô distribuirá três tipos de bala: de morango, de laranja ou de hortelã. A cada nova rodada, somente uma bala será dada pelo robô a cada criança, partindo-se da criança A até a criança E, em ordem alfabética, conforme ilustrado na figura a seguir.

A distribuição das balas seguirá a seguinte rotina, a qual será obedecida também quando se passar de uma rodada para outra: se uma criança receber uma bala de morango, a criança seguinte receberá uma bala de laranja; se uma criança receber uma bala de laranja, a criança seguinte receberá uma bala de hortelã; se uma criança receber uma bala de hortelã, a criança seguinte receberá uma bala de morango.
A partir dessa situação hipotética, julgue os itens seguintes, considerando que a criança A receberá uma bala de morango na primeira rodada.
As chances de que, após 92 rodadas, todas as cinco crianças tenham recebido, pelo menos, 30 balas do mesmo sabor são superiores a 75%.
Em uma loja há entre 30 e 50 troféus em miniatura. A funcionária da loja agrupou-os de 5 a 5 e sobrou-lhe um troféu. Depois, agrupou-os de 3 a 3 e não sobrou nenhum troféu. O número exato de troféus na loja é:
Treze cadeiras numeradas consecutivamente de 1 a 13 formam uma fila. Quatro pessoas devem sentar-se nelas e o número da cadeira em que cada uma deve se sentar será decidido por sorteio. Para as três primeiras pessoas foram sorteados os números 3, 8 e 11 e será feito o sorteio para a última cadeira a ser ocupada.
A probabilidade de que a quarta pessoa NÃO se sente ao lado de nenhuma pessoa já sentada é:
Em uma feira de ciências, cinco crianças, designadas pelas letras A, B, C, D e E, participarão de um experimento no qual um robô distribuirá três tipos de bala: de morango, de laranja ou de hortelã. A cada nova rodada, somente uma bala será dada pelo robô a cada criança, partindo-se da criança A até a criança E, em ordem alfabética, conforme ilustrado na figura a seguir.

A distribuição das balas seguirá a seguinte rotina, a qual será obedecida também quando se passar de uma rodada para outra: se uma criança receber uma bala de morango, a criança seguinte receberá uma bala de laranja; se uma criança receber uma bala de laranja, a criança seguinte receberá uma bala de hortelã; se uma criança receber uma bala de hortelã, a criança seguinte receberá uma bala de morango.
A partir dessa situação hipotética, julgue os itens seguintes, considerando que a criança A receberá uma bala de morango na primeira rodada.
Ao final da rodada de número 30, a criança C terá recebido exatamente 10 balas de morango
As festas juninas são festas tradicionais que ocorrem em todo o país e possuem, além de muita comida e dança, brincadeiras e competições. Por isso, são ambientes excelentes para problemas de contagem e probabilidade e para estudos de fenômenos aleatórios. Com relação a esse tema, julgue o item que se segue.
Situação hipotética: Quatro equipes de dança — E1, E2, E3 e E4 — estão competindo no concurso de melhor quadrilha de uma festa junina. Sabe-se que as equipes E1 e E4 têm chances iguais de vencer a competição e que a equipe E3 tem duas vezes mais chances de vencer o concurso que a equipe E2. Sabe-se, também, que a probabilidade de que a equipe E1 ou a equipe E3 vença é de 60%. Assertiva: Nessa situação, a probabilidade de a equipe E3 vencer o concurso de quadrilhas é de 20%.


