Cada um dos itens a seguir apresenta uma situação hipotética seguida de uma assertiva a ser julgada com base em análise combinatória, probabilidade, operações com conjuntos e problemas geométricos.
Considere que 44 servidores falem uma ou mais línguas estrangeiras e que, entre eles, 12 servidores falem apenas inglês; 10 falem apenas espanhol; 11 falem apenas francês; 1 fale inglês e francês; 2 falem espanhol e francês; e 17 falem francês. Nessa situação, 7 servidores falam inglês e espanhol, mas não falam francês.
Ao realizar o cadastro em um aplicativo de investimentos, foi i solicitado ao usuário que criasse uma senha, sendo
permitido o uso somente dos seguintes caracteres:
• algarismos de 0 a 9;
• 26 letras minúsculas do alfabeto;
• 26 letras maiúsculas do alfabeto;
• 6 caracteres especiais !, @, #, $, , &.
Três tipos de estruturas para senha foram apresentadas ao usuário:
• tipo I: formada por quaisquer quatro caracteres
distintos, escolhidos dentre os permitidos;
• tipo II: formada por cinco caracteres distintos,
iniciando por três letras, seguidas por um algarismo
e, ao final, um caractere especial;
• tipo III: formada por seis caracteres distintos, iniciando
por duas letras, seguidas por dois algarismos e, ao
final, dois caracteres especiais.
Considere p1, p2 e p3 as probabilidades de se descobrirem ao acaso, na primeira tentativa, as senhas dos tipos I, II e III, respectivamente.
Nessas condições, o tipo de senha que apresenta a menor probabilidade de ser descoberta ao acaso, na primeira tentativa, é o
Numa sala há 25 carteiras dispostas em 5fileiras com 5 carteiras cada numeradas daseguinte forma: Na primeira fila as carteiras vão
de número 1 a 5, na segunda fileira as carteiras vão de 6 a 10, na terceira fileira as carteiras vão de 11 a 15, na quarta fileira as carteiras vão de 16 a 20 e na última fileira as carteiras vão de 21 a 25.
Nessas condições, a probabilidade de uma pessoa estar sentada numa carteira de número par, sabendo que essa carteira não é da terceira fileira, é igual a:
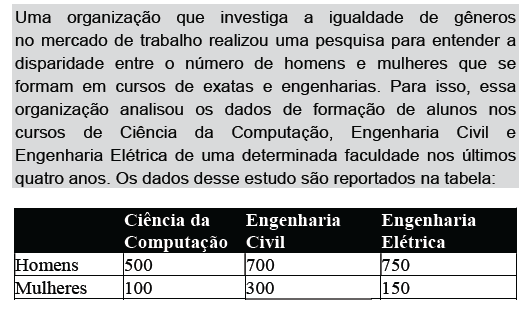
Dadas as afirmativas com relação aos dados coletados,
I. A taxa de pessoas do sexo feminino formadas no curso de Ciência da Computação é de 20%.
II. Apenas 22% das pessoas formadas nesses três cursos são do sexo feminino.
III. A chance de uma pessoa desse grupo, sorteada ao acaso, ser mulher, formada em Ciência da Computação, ou mulher, formada em Engenharia Elétrica, é de apenas 10%.
IV. O curso de Engenharia Civil forma, proporcionalmente, menos mulheres do que homens na comparação entre os três cursos.
verifica-se que estão corretas apenas
O gestor constatou que 3 agentes de pesquisa por telefone, A, B e C, foram responsáveis por 20%, 50% e 30%, respectivamente, do volume total de informação coletada durante um dia. Esses agentes costumam apresentar inconsistência de 20%, 5% e 2%, respectivamente, entre as informações coletadas e as prestadas pelos informantes. Escolheu-se aleatoriamente uma informação coletada e verificou-se que era inconsistente. A probabilidade de ter sido coletada pelo agente A é, aproximadamente, igual a:
Na tabela a seguir, estão os dados de 74 funcionários do setor de comunicação de uma empresa, quanto ao gênero e ao consumo ou não de café:
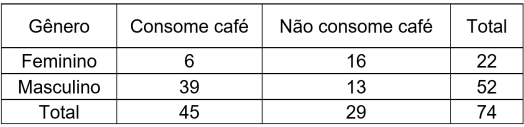
Se um funcionário desse setor for sorteado, a probabilidade de que este consuma café, sabendo que é do gênero feminino, é igual a:
No alojamento de uma universidade, há alguns quartos com o padrão superior ao dos demais. Um desses quartos ficou disponível, e muitos estudantes se candidataram para morar no local. Para escolher quem ficará com o quarto, um sorteio será realizado. Para esse sorteio, cartões individuais com os nomes de todos os estudantes inscritos serão depositados em uma urna, sendo que, para cada estudante de primeiro ano, será depositado um único cartão com seu nome; para cada estudante de segundo ano, dois cartões com seu nome; e, para cada estudante de terceiro ano, três cartões com seu nome. Foram inscritos 200 estudantes de primeiro ano, 150 de segundo ano e 100 de terceiro ano. Todos os cartões têm a mesma probabilidade de serem sorteados.
Qual a probabilidade de o vencedor do sorteio ser um estudante de terceiro ano?
Em uma competição esportiva, o time A enfrentará o time B quatro vezes seguidas. Em cada uma das partidas, a probabilidade de que o time A vença o time B é 0,6.
A probabilidade de que o time A vença apenas duas vezes é de
Marcelo joga, simultaneamente, dois dados cúbicos honestos cujas faces estão numeradas de 1 a 6.
A probabilidade de os dois números sorteados serem consecutivos é:
Gabriela comprou um novo carro que pode ser abastecido tanto com gasolina, álcool ou com os dois. Sabe-se que Gabriela abastece sempre uma vez por semana, que abastece apenas com gasolina um terço das vezes, somente com álcool metade das vezes, e com uma mistura dos dois um sexto das vezes.
A probabilidade de ela ter abastecido com alguma quantidade álcool hoje é de:
Oito amigos sentam-se, ao acaso, ao redor de uma mesa retangular com 4 lugares em cada um dos lados mais longos. A probabilidade de Ana e Abel ficarem sentados em frente um do outro é:
As festas juninas são festas tradicionais que ocorrem em todo o país e possuem, além de muita comida e dança, brincadeiras e competições. Por isso, são ambientes excelentes para problemas de contagem e probabilidade e para estudos de fenômenos aleatórios. Com relação a esse tema, julgue o item que se segue.
Situação hipotética: O público de determinada festa junina é formado por 60% de mulheres e 40% de homens. Desse público, sabe-se que 35% das mulheres compraram a rifa de São João, enquanto a porcentagem dos homens que a compraram foi de 45%. Assertiva: Nessa situação, a probabilidade de que um participante da festa que comprou a rifa de São João seja mulher é superior a 50%.
A seguir, são apresentadas informações obtidas a partir de uma pesquisa realizada com 1.000 pessoas.
• 480 possuem plano de previdência privada;
• 650 possuem aplicações em outros tipos de produtos financeiros;
• 320 não possuem aplicação em nenhum produto financeiro.
Com base nessa situação hipotética, julgue o item seguinte.
Se uma pessoa escolhida ao acaso entre as que participaram da pesquisa possui plano de previdência privada, então a probabilidade de ela possuir também aplicação em outros produtos financeiros é superior a 90%.
Uma caixa contém 4 bolas numeradas 1, 2, 3 e 4. Selecionam-se, ao acaso, 2 bolas sem reposição.
A probabilidade de 3 ser o maior número selecionado é
Em uma caixa, foram depositadas 500 bolas idênticas e numeradas de 1 a 500. Qual a probabilidade de, ao ser sorteada aleatoriamente uma dessas bolas, o número que esteja impresso na bola seja diferente de um múltiplo de 7 e 9, simultaneamente?

