Um piscicultor cria uma espécie de peixe em um tanque cilíndrico. Devido às características dessa espécie, o tanque deve ter, exatamente, 2 metros de profundidade e ser dimensionado de forma a comportar 5 peixes para cada metro cúbico de água. Atualmente, o tanque comporta um total de 750 peixes. O piscicultor deseja aumentar a capacidade do tanque para que ele comporte 900 peixes, mas sem alterar a sua profundidade. Considere 3 como aproximação para π.
O aumento da medida do raio do tanque, em metro, deve ser de
A taxa de mortalidade infantil vem decaindo a cada ano no Brasil. O gráfico, gerado a partir de dados do IBGE, apresenta a evolução da taxa de mortalidade infantil (número de óbitos para cada 1 000 nascidos vivos) de crianças com até 5 anos, no Brasil, no período de 2000 a 2011.
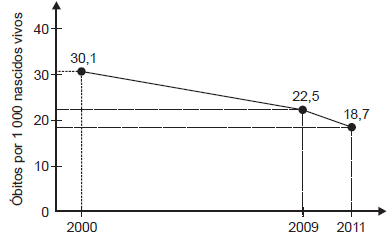
Considere que, para os próximos anos, o decréscimo anual médio do número de óbitos para cada 1 000 nascidos vivos registrado, no período de 2009 a 2011, será mantido.
A partir das informações fornecidas, a taxa de mortalidade infantil de crianças com até 5 anos tornar-se-á inferior a 10 no período de
Para um docente estrangeiro trabalhar no Brasil, ele necessita validar o seu diploma junto ao Ministério da Educação. Num determinado ano, somente para estrangeiros que trabalharão em universidades dos estados de São Paulo e Rio de Janeiro, foram validados os diplomas de 402 docentes estrangeiros. Na tabela, está representada a distribuição desses docentes estrangeiros, por países de origem, para cada um dos dois estados.
A probabilidade de se escolher, aleatoriamente, um docente espanhol, sabendo-se que ele trabalha em uma universidade do estado de São Paulo é
Para uma reportagem, dispondo das velocidades recordes da tartaruga e do caramujo em metro por segundo, se faz necessário saber o fator de conversão da velocidade recorde da lesma para metro por segundo para divulgar uma comparação.
Com base nas informações, o fator de conversão da velocidade recorde da lesma para metro por segundo é
A fim de reforçar o orçamento familiar, uma dona de casa começou a produzir doces para revender. Cada receita é composta de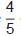 
de quilograma de amendoim e 
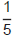de quilograma de açúcar.
O quilograma de amendoim custa R$ 10,00 e o do açúcar, R$ 2,00. Porém, o açúcar teve um aumento e o quilograma passou a custar R$ 2,20. Para manter o mesmo custo com a produção de uma receita, essa dona de casa terá que negociar um desconto com o fornecedor de amendoim.
Nas condições estabelecidas, o novo valor do quilograma de amendoim deverá ser igual a
O dono de uma loja pretende usar cartões imantados para a divulgação de sua loja. A empresa que fornecerá o serviço lhe informa que o custo de fabricação do cartão é de R$ 0,01 por centímetro quadrado e que disponibiliza modelos tendo como faces úteis para impressão:
- um triângulo equilátero de lado 12 cm;
- um quadrado de lado 8 cm;
- um retângulo de lados 11 cm e 8 cm;
- um hexágono regular de lado 6 cm;
- um círculo de diâmetro 10 cm.
O dono da loja está disposto a pagar, no máximo, R$ 0,80 por cartão. Ele escolherá, dentro desse limite de preço, o modelo que tiver maior área de impressão.
Use 3 como aproximação para π e use 1,7 como aproximação para .
Nessas condições, o modelo que deverá ser escolhido tem como face útil para impressão um
Um povoado com 100 habitantes está passando por uma situação de seca prolongada e os responsáveis pela administração pública local decidem contratar a construção de um reservatório. Ele deverá ter a forma de um cilindro circular reto, cuja base tenha 5 metros de diâmetro interno, e atender à demanda de água da população por um período de exatamente sete dias consecutivos. No oitavo dia, o reservatório vazio é
completamente reabastecido por carros-pipa.
Considere que o consumo médio diário por habitante é de 120 litros de água. Use 3 como aproximação para π.
Nas condições apresentadas, o reservatório deverá ser construído com uma altura interna mínima, em metro, igual a
Um atleta produz sua própria refeição com custo fixo de R$ 10,00. Ela é composta por 400 g de frango, 600 g de batata-doce e uma hortaliça. Atualmente, os preços dos produtos para essa refeição são:
Em relação a esses preços, haverá um aumento de 50% no preço do quilograma de batata-doce, e os outros preços não serão alterados. O atleta deseja manter o custo da refeição, a quantidade de batata-doce e a hortaliça. Portanto, terá que reduzir a quantidade de frango.
Qual deve ser a redução percentual da quantidade de frango para que o atleta alcance seu objetivo?
A receita R de uma empresa ao final de um mês é o dinheiro captado com a venda de mercadorias ou com a prestação de serviços nesse mês, e a despesa D é todo o dinheiro utilizado para pagamento de salários, contas de água e luz, impostos, entre outros. O lucro mensal obtido ao final do mês é a diferença entre a receita e a despesa registradas no mês. O gráfico apresenta as receitas e despesas, em milhão de real, de uma empresa ao final dos cinco primeiros meses de um dado ano.
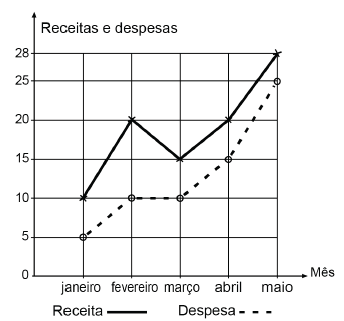
A previsão para os próximos meses é que o lucro mensal não seja inferior ao maior lucro obtido até o mês de maio.
Nessas condições, o lucro mensal para os próximos meses deve ser maior ou igual ao do mês de
Um casal está planejando comprar um apartamento de dois quartos num bairro de uma cidade e consultou a página de uma corretora de imóveis, encontrando 105 apartamentos de dois quartos à venda no bairro desejado. Eles usaram um aplicativo da corretora para gerar a distribuição dos preços do conjunto de imóveis selecionados.
O gráfico ilustra a distribuição de frequências dos preços de venda dos apartamentos dessa lista (em mil reais), no qual as faixas de preço são dadas por ]300, 400], ]400, 500], ]500, 600], ]600, 700], ]700, 800], ]800, 900], ]900, 1 000], ]1 000, 1 100], ]1 100, 1 200] e ]1 200, 1 300].
A mesma corretora anuncia que cerca de 50% dos apartamentos de dois quartos nesse bairro, publicados em sua página, têm preço de venda inferior a 550 mil reais. No entanto, o casal achou que essa última informação não era compatível com o gráfico obtido.
Com base no gráfico obtido, o menor preço, p (em mil reais), para o qual pelo menos 50% dos apartamentos apresenta preço inferior a p é
Em um estudo realizado pelo IBGE em quatro estados e no Distrito Federal, com mais de 5 mil pessoas com 10 anos ou mais, observou-se que a leitura ocupa, em média, apenas seis minutos do dia de cada pessoa. Na faixa de idade de 10 a 24 anos, a média diária é de três minutos. No entanto, no grupo de idades entre 24 e 60 anos, o tempo médio diário dedicado à leitura é de 5 minutos. Entre os mais velhos, com 60 anos ou mais, a média é de 12 minutos.
A quantidade de pessoas entrevistadas de cada faixa de idade seguiu a distribuição percentual descrita no quadro.
Os valores de x e y do quadro são, respectivamente, iguais a
Um segmento de reta está dividido em duas partes na proporção áurea quando o todo está para uma das partes na mesma razão em que essa parte está para a outra. Essa constante de proporcionalidade é comumente representada pela letra grega φ, e seu valor é dado pela solução positiva da equação φ2 = φ + 1.
Assim como a potência φ2, as potências superiores de φ podem ser expressas da forma aφ + b, em que a e b são inteiros positivos, como apresentado no quadro.
A potência φ7 , escrita na forma aφ + b (a e b são inteiros positivos), é
Os diretores de uma escola precisam construir um laboratório para uso dos alunos. Há duas possibilidades:
(i) um laboratório do tipo A, com capacidade para 100 usuários, a um custo de 180 mil reais e gastos de 60 mil reais por ano para manutenção;
(ii) um laboratório do tipo B, com capacidade para 80 usuários, a um custo de 120 mil reais e gastos com manutenção de 16 mil reais por ano.
Considera-se que, em qualquer caso, o laboratório implantado será utilizado na totalidade de sua capacidade.
A economia da escola, na utilização de um laboratório tipo B, em vez de um laboratório tipo A, num período de 4 anos, por usuário, será de
Uma pessoa comprou uma caneca para tomar sopa, conforme ilustração.
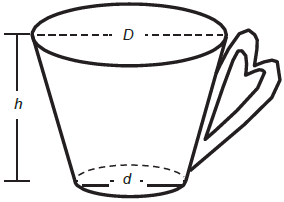
Sabe-se que 1 cm3 = 1 mL e que o topo da caneca é uma circunferência de diâmetro (D) medindo 10 cm, e a base é um círculo de diâmetro (d) medindo 8 cm. Além disso, sabe-se que a altura (h) dessa caneca mede 12 cm (distância entre o centro das circunferências do topo e da base).
Utilize 3 como aproximação para π.
Qual é a capacidade volumétrica, em mililitro, dessa caneca?
O projeto de um contêiner, em forma de paralelepípedo reto retangular, previa a pintura dos dois lados (interno e externo) de cada uma das quatro paredes com tinta acrílica e a pintura do piso interno com tinta epóxi. O construtor havia pedido, a cinco fornecedores diferentes, orçamentos das tintas necessárias, mas, antes de iniciar a obra, resolveu mudar o projeto original, alterando o comprimento e a largura para o dobro do originalmente previsto, mantendo inalterada a altura. Ao pedir novos orçamentos aos fornecedores, para as novas dimensões, cada um deu uma resposta diferente sobre as novas quantidades de tinta necessárias.
Em relação ao previsto para o projeto original, as novas quantidades de tinta necessárias informadas pelos fornecedores foram as seguintes:
- Fornecedor I: “O dobro, tanto para as paredes quanto para o piso.”
- Fornecedor II: “O dobro para as paredes e quatro vezes para o piso.”
- Fornecedor III: “Quatro vezes, tanto para as paredes quanto para o piso.”
- Fornecedor IV: “Quatro vezes para as paredes e o dobro para o piso.”
- Fornecedor V: “Oito vezes para as paredes e quatro vezes para o piso.”
Analisando as informações dos fornecedores, o construtor providenciará a quantidade adequada de material. Considere a porta de acesso do contêiner como parte de uma das paredes.
Qual dos fornecedores prestou as informações adequadas, devendo ser o escolhido pelo construtor para a aquisição do material?
