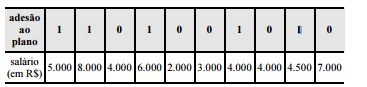
Considerando que os dados na tabela mostram salários de diferentes servidores que aderiram (1) ou não aderiram (0) a determinado plano de previdência complementar, julgue os itens subsecutivos.
Um modelo de regressão logística só aceita variáveis
categóricas; um modelo de regressão linear só aceita
variáveis quantitativas.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:
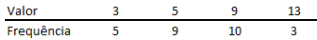
Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Considerando-se que apenas os 10% que atinjam as maiores notas serão aprovados, a nota mínima para aprovação é:
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
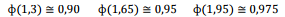
Onde,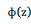 é a função distribuição acumulada da Normal Padrão.
é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
A função geradora de momentos M(t ) de uma variável aleatória X é definida para todos os valores reais de t como M(t )=E[etx]. Assinale a função geradora de momentos da distribuição Normal com média 0 e desvio-padrão 1.
Considerando fx(x ) a função densidade de probabilidade de uma variável aleatória X, analise as afirmativas a seguir.

Está(ão) correta(s) apenas a(s) afirmativa(s)
Sobre Modelos Lineares Generalizados (MLG), analise as afirmativas, marque V para as verdadeiras e F para as falsas.

A sequência está correta em
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X²) = 25, E( X) = 4, Var (X ) = 16, Cov(X,Y ) .
Então a variância de Z é:
Sabe-se que as notas de uma prova têm distribuição Normal
com média μ = 6,5 e variância α = 4²
. Adicionalmente, são
conhecidos alguns valores tabulados da normal-padrão.
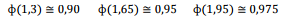
Onde,
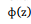
é a função distribuição acumulada da Normal Padrão.
Considerando-se que apenas os 10% que atinjam as maiores notas
serão aprovados, a nota mínima para aprovação é:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Após a extração de uma amostra, as observações obtidas são
tabuladas, gerando a seguinte distribuição de frequências:

Considerando que E(X ) = Média de X, Mo(X ) = Moda de X e Me(X )
= Mediana de X, é correto afirmar que:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X²) = 25, E( X) = 4, V (X )= 16, (X,Y )= 6.
Então a variância de Z é:
Sejam Y, X, Z e W variáveis aleatórias tais que Z = 2.Y - 3.X,
sendo E(X²) = 25, E( X) = 4, V ( X) = 16,Cov (X,Y ) = 6 .
Então a variância de Z é:



