Ivan usa sua calculadora para gerar números aleatórios entre 0 e 3. Ele está interessado em calcular a sua diferença. Qual a probabilidade de que a diferença obtida seja maior que 2?
Em 1.º de janeiro de 2010, o gerente de uma grande rede de supermercados resolve fazer uma liquidação de TV de plasma de 26", com desconto de 40% no pagamento à vista, dando garantia de funcionamento até a Copa de 2014. O gerente sabe que a duração desses televisores tem distribuição normal com média de 2.000 dias e desvio padrão de 200 dias. Com essa liquidação, o gerente almeja vender 1.000 unidades. Considerando um ano como tendo 365 dias, quantos aparelhos de TV de plasma de 26" devem ser trocados pelo uso da garantia dada até a Copa de 2014?
Considerando o período de 1988 a 2008, a moda da variável X foi igual a 254.
O número de casos diários de desordens musculoesqueléticas (W) em certa empresa é uma variável aleatória discreta que segue uma distribuição condicional na forma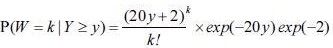 
, em que Y é uma variável aleatória contínua tal que 
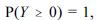k = 0, 1, 2, ... e exp(!2) = 0,137.
R. Quintana e I. Pawlowitz. Safety Science, 32, 1999, p. 19-31 (com adaptações).
Com base nessas informações, julgue os itens subsequentes.
A probabilidade P(W = 1) é superior a 0,12 e inferior a 0,16.
Um estudo mostrou que o tempo de ocupação de um leito hospitalar - T -, em horas, segue uma distribuição cuja função de densidade é expressa por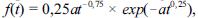 
em que a > 0 é um parâmetro fixo e t > 0.
M.D. Banks et alli. Clinical Nutrition, 2009, p. 1-7 (com adaptações).
Com base nessas informações, julgue os itens seguintes.
A função de densidade f(t) assume apenas valores entre 0 e 1.
O primeiro momento central da variável aleatória T é igual a zero, enquanto o segundo momento central dessa mesma distribuição corresponde à variância dos tempos.
A média de uma distribuição t de Student é igual a zero.
A probabilidade de significância pode ser interpretada como sendo muito baixa a probabilidade de se obter um valor da estatística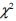 
superior a 28,71, assim é correto inferir que a proporção das pacientes do grupo caso difere da proporção das pacientes do grupo controle.
A estatística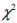 
tem distribuição quiquadrado com 
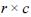graus de liberdade, em que r é o número de linhas da tabela e c é o número de colunas.
Uma população de plantas contém 3 diferentes genótipos: A, B e C, com as respectivas proporções: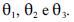 
Em um estudo em que 100 plantas dessa população foram registradas no cerrado, observou-se o número de plantas associadas a cada genótipo: 32, 57 e 11. De acordo com a literatura científica da área, as proporções esperadas são iguais a 30%, 50% e 20%.
Considerando essas informações, julgue os itens que se seguem.
Para se obterem os estimadores de máxima verossimilhança para 
deve-se maximizar a função 
Considerando que o tamanho da amostra seja pequeno, para se testar a hipótese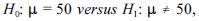 
deve-se utilizar o teste-t. Esse tipo de procedimento é adequado para modelar a distribuição amostral da média aritmética dos tempos de sobrevida dos pacientes.
Os parâmetros a e b são obtidos resolvendo-se o sistema de equações lineares a seguir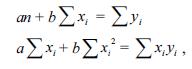
em que n representa o tamanho da amostra.
No caso específico em que a = 0, as equações normais são expressas por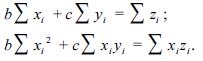
Na amostragem aleatória simples, a relação entre o tamanho mínimo da amostra - n - e o tamanho da população - N - é dada por n =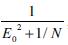 
em que 
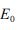representa o erro amostral E 1/ N 1 2 0 + tolerável. Com base nessas informações, julgue os itens seguintes.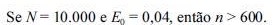
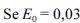, então o tamanho n = 1.000 de uma amostra é suficientemente grande para qualquer tamanho N da população.
