Um engenheiro realizou pesquisa em que analisou a relação entre a quantidade de curvas de um trecho de serra (X) e o tempo gasto em minutos (Y) por veículos de passeio — em que Y seja a variável resposta e X, a variável regressora —, com o objetivo de propor soluções que permitam diminuir o tempo gasto por esses veículos. A tabela abaixo apresenta os resultados da análise de variância (ANOVA) do modelo de regressão linear simples na forma Y = α + βX + g, em que α e β são os coeficientes do modelo e g representa o erro aleatório.
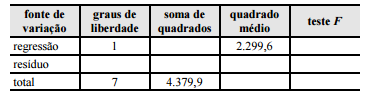
Considerando a situação hipotética e a tabela acima apresentadas, julgue os itens que se seguem
Em face dessa situação, é correto afirmar que o coeficiente de
determinação R² será superior a 50%.
Um engenheiro realizou pesquisa em que analisou a relação entre a quantidade de curvas de um trecho de serra (X) e o tempo gasto em minutos (Y) por veículos de passeio — em que Y seja a variável resposta e X, a variável regressora —, com o objetivo de propor soluções que permitam diminuir o tempo gasto por esses veículos. A tabela abaixo apresenta os resultados da análise de variância (ANOVA) do modelo de regressão linear simples na forma Y = α + βX + g, em que α e β são os coeficientes do modelo e g representa o erro aleatório.
Considerando a situação hipotética e a tabela acima apresentadas, julgue os itens que se seguem
Caso o engenheiro deseje saber se o gênero do motorista
exerce influência no tempo gasto no trecho, bastará incluir uma
variável dicotômica do tipo 0 e 1 ou 1 e 2.
Um engenheiro realizou pesquisa em que analisou a relação entre a quantidade de curvas de um trecho de serra (X) e o tempo gasto em minutos (Y) por veículos de passeio — em que Y seja a variável resposta e X, a variável regressora —, com o objetivo de propor soluções que permitam diminuir o tempo gasto por esses veículos. A tabela abaixo apresenta os resultados da análise de variância (ANOVA) do modelo de regressão linear simples na forma Y = α + βX + g, em que α e β são os coeficientes do modelo e g representa o erro aleatório.
Considerando a situação hipotética e a tabela acima apresentadas, julgue os itens que se seguem
A variância amostral de X poderá ser obtida dividindo-se a
soma de quadrados da regressão pelo quadrado da estimativa
do parâmetro β, e depois se dividindo esse resultado pelo
número de graus de liberdade total.
Imagine um conjunto de dados referente a uma variável quantitativa. Todos os valores do conjunto são iguais a 4.
Neste caso, a média, a mediana e o desvio padrão do conjunto seriam, respectivamente:
Considere que um modelo de regressão qualquer gerou resíduos padronizados que estão representados no diagrama de dispersão a seguir, em função dos valores da variável independente: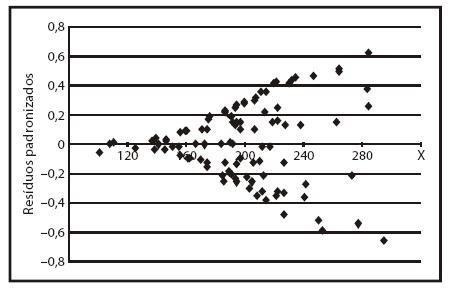
Sobre o modelo de regressão que gerou os resíduos padronizados mostrados no diagrama acima, pode-se afirmar que:
Seja X uma variável aleatória contínua com média igual a ?. Utilizando o teorema de Tchebyshev, obteve-se a probabilidade mínima de que X pertença ao intervalo (? ? 1,6; ? + 1,6) igual a 36%. O valor do desvio padrão de X é igual a
Considere uma amostra de 8 elementos proveniente de uma população com função densidade f(x) =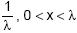 
Com base nesta amostra, apurou-se que o estimador de máxima verossimilhança da variância da população foi igual a 3. O maior valor apresentado nesta amostra foi
O objetivo de um estudo realizado em duas cidades X e Y foi apurar, com relação a um determinado assunto, o nível de atendimento oferecido aos seus habitantes. Cada cidade possui um posto de atendimento e cada posto atende somente aos habitantes de sua cidade. Em cada cidade foram sorteados aleatoriamente 12 habitantes atendidos pelo respectivo posto. O resultado pode ser visualizado pela tabela abaixo.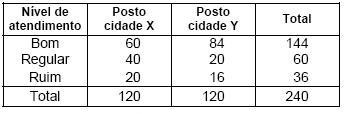
Utilizou-se o teste qui-quadrado para avaliar se existe diferença no nível de atendimento dos postos das duas cidades. O valor observado do qui-quadrado e o número correspondente dos graus de liberdade do teste são, respectivamente, iguais a
A probabilidade de que um item produzido por uma máquina seja defeituoso é 10%. Uma amostra de 40 itens produzidos por esta máquina é selecionada ao acaso. Usando-se a aproximação pela distribuição de Poisson para determinar a probabilidade de que não mais que dois itens defeituosos sejam encontrados na amostra, obtemos
Em um pequeno grupo de casais, X e Y são as variáveis aleatórias que representam a renda, em milhares de reais, do marido e de sua esposa, respectivamente. A distribuição de probabilidade conjunta de X e Y é dada na tabela abaixo: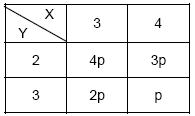
Seja Z = 0,7X + 0,8Y a renda do casal após a dedução de impostos. A média de Z, em milhares de reais, é
Sabe-se que as variáveis aleatórias X e Y são independentes e que ambas são normalmente distribuídas da seguinte forma: X: N(80,100) e Y: N(50, 96). Fazendo uso da informação que P(0 < Z < 1,48) = 0,43, onde Z é a normal padrão, o valor de K para que P ([X ? Y]) >K) = 0,93 é
Dr. Carlos Eduardo é um médico que trabalha no programa
Médico da Família. A partir dos registros dos prontuários dos
pacientes atendidos pelo programa, ele montou a seguinte
distribuição das idades (em anos completos) de uma amostra
de mães:
Em um hotel fazenda, o gerente registra as despesas por dia
de estada (Y) de seus clientes durante o tempo (X) em que
estão hospedados. Uma amostra das despesas relativas a
oito dessas diárias está na tabela seguinte:
O gerente percebeu que as despesas totais de estada
seguem um modelo linear. Para esses dados, obteve: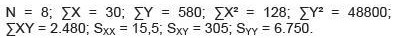
O coeficiente de correlação do modelo linear é
O tempo médio de audiência (TMA) é um indicador do tempo
que os ouvintes dedicaram a um programa em determinado
horário. Considere os dados da tabela seguinte.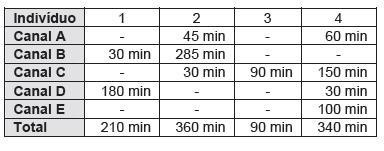
Um índice de fidelidade (IF) pode ser definido assim: para cada indivíduo, verifica-se o percentual de tempo que foi dedicado ao programa (ou canal), e a média desses valores determina a Audiência Média (AM); o percentual de espectadores (%E) que assistiram ao programa (canal). Daí, IF = 100 × AM / %E. Para o canal E, o IF é de aproximadamente
Um professor de probabilidade aplica a seus alunos
um teste com questões de múltipla escolha de quatro
alternativas (A, B, C, D), sendo apenas uma verdadeira. O
discente deve seguir as instruções: ele pode escolher até
quatro alternativas para ganhar três pontos na marcação
certa e perde um ponto por marcação errada.
Para obter a melhor pontuação por questão, o número de marcações que o aluno deve fazer, em cada uma delas, é
