Relativamente às metodologias de análise vertical e horizontal, julgue o item seguinte
Se um item patrimonial apresentar um saldo negativo de R$ 10 em dado período e o número índice que representa a relação desse saldo com o saldo do exercício subsequente for igual a –12,5, então é correto concluir que terá havido uma inversão no sinal da conta.
Relativamente às metodologias de custeio para fins de avaliação de estoques e para a tomada de decisões, julgue o item que se segue.
A implantação de um sistema de custo-padrão em uma empresa diminui o volume de trabalho envolvido no processo de custeamento e no de controle de custos, visto que os padrões são preestabelecidos, o que facilita tais procedimentos.
Com relação ao estudo da relação custo versus volume versus lucro, julgue o próximo item.
Considere-se que certa empresa deveria atingir seu ponto de equilíbrio contábil ao faturar R$ 5 milhões com a venda de seu único produto, tendo, contudo, obtido prejuízo societário de R$ 300 mil, apesar de não ter havido variação em sua estrutura de custos e preços. Nessa situação, dado que os estoques da empresa estavam zerados no início do período, uma explicação possível para essa contradição é a de que houve aumento no estoque de produtos
Com respeito ao conjunto de dados {0, 0, 1, 1, 1, 3}, julgue o item que se segue.
Se esse conjunto de dados fosse representado por um diagrama de box-plot, então os valores 0 e 3 seriam chamados valores exteriores, ou, ainda, discrepantes, atípicos ou outliers.
Suponha que o conjunto de dados mostrados no quadro acima seja uma realização de uma amostra aleatória simples de tamanho n = 5 que foi retirada de uma população cuja função de densidade de probabilidade é dada por
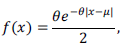
na qual x ∈ ℝ, e θ > 0 e μ ℝ são parâmetros desconhecidos. Com base nessas informações, julgue os itens subsequentes.
A estimativa de máxima verossimilhança da moda populacional é igual a 10,6.
Suponha que o conjunto de dados mostrados no quadro acima seja uma realização de uma amostra aleatória simples de tamanho n = 5 que foi retirada de uma população cuja função de densidade de probabilidade é dada por
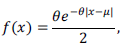
na qual x ∈ ℝ, e θ > 0 e μ ℝ são parâmetros desconhecidos. Com base nessas informações, julgue os itens subsequentes.
Se X for definida como uma variável aleatória que representa a distribuição populacional em tela e se p = P (X = 10,6), então a estimativa dessa probabilidade será = 2/5.
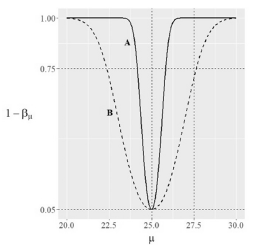
Considerando que a figura acima mostra as curvas de poder referentes a dois testes de hipóteses - A (linha contínua) e B (linha tracejada) - para a média populacional μ, julgue o item a seguir.
Com respeito ao teste de hipóteses B, se μ = 27,5, então a probabilidade de se rejeitar a hipótese nula será inferior a 0,75.
Considerando que a função de densidade conjunta do par de variáveis aleatórias (X,Y) seja dada por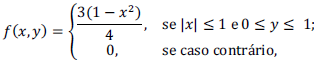 
julgue os próximo item.
, em que
Considerando que X1, X2, …Xn seja uma sequência de variáveis aleatórias independentes e identicamente distribuídas, tais que em que x { 0, 1, 2, 3, …}, julgue o item a seguir.
Se , então, segundo a lei fraca dos grandes números, converge em probabilidade para
Considerando que X1, X2, …Xn seja uma sequência de variáveis aleatórias independentes e identicamente distribuídas, tais que em que x { 0, 1, 2, 3, …}, julgue o item a seguir.
Supondo que para y {0, 1, 2, 3…}, em que m > 0, e M é uma variável aleatória contínua cuja função de densidade é dada por FM(m) = e-m , julgue o item a seguir
são variáveis aleatórias independentes
O quadro a seguir mostra as estimativas de mínimos quadrados ordinários dos coeficientes de um modelo de regressão linear simples na forma , em que i ∈ {1, ..., 6} e representa o erro aleatório com média zero e variância .
Considerando essas informações e sabendo que = 0,01, julgue o item seguinte.
O coeficiente de determinação do modelo (R2) é igual a 0,8
Considerando que yk denote o valor ajustado - pelo método de mínimos quadrados ordinários - da variável resposta yk de um modelo de regressão linear múltipla na forma para K ∈ {1,…,10}; que, nesse modelo,{∈1, … , ∈10} seja um conjunto de erros aleatórios independentes com médias iguais a zero e variâncias iguais a ; e que cada resíduo produzido pelo ajuste seja escrito como julgue o próximo item.
A estatística é uma estatística qui-quadrado que permite avaliar a falta de ajuste (lack-of-fit) do modelo ajustado.
A tabela ANOVA a seguir se refere ao ajuste de um modelo de regressão linear simples escrito como y = a + bx + ∈, cujos coeficientes foram estimados pelo método da máxima verossimilhança, com . Os erros em torno da reta esperada são independentes e identicamente distribuídos.
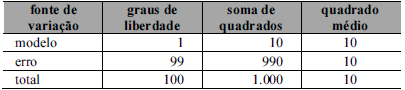
Com base nessas informações, julgue o item a seguir.
Para se testar a hipótese nula contra a hipótese alternativa , a estatística do teste F proporcionada pela tabela ANOVA é igual ou superior a 2.
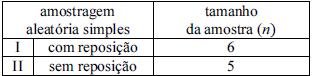
Suponha que determinada população de tamanho N = 100 seja constituída pelos elementos x1, ..., x100. Para a realização de um levantamento amostral sobre essa população, cogitam-se duas possibilidades mostradas no quadro anterior, ambas pelo método de amostragem aleatória simples. Se o tipo I for o escolhido, então a amostragem será com reposição com n = 6. No entanto, se o escolhido for o tipo II, então a amostra será sem reposição com n = 5.
Com base nessas informações, julgue o item que se segue.
Se o tipo II for aplicado, a probabilidade de que a amostra seja formada pelos elementos x8, x27, x70, x77, x99 é igual a
