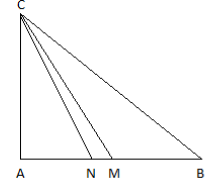
Para fazer um projeto de rede elétrica, seria necessário saber a distância entre os postes, e a presença do lago impedia a medição direta dessa distância. Um engenheiro posicionou-se em um local onde era possível visualizar os dois postes e medir a distância entre eles. Com os equipamentos apropriados, realizou as medidas e fez o seguinte esboço, chamando de d a distância entre os postes.
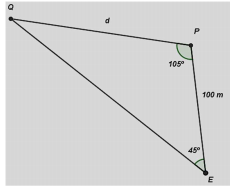
A distância d entre os postes é
O gráfico abaixo representa uma função trigonométrica.
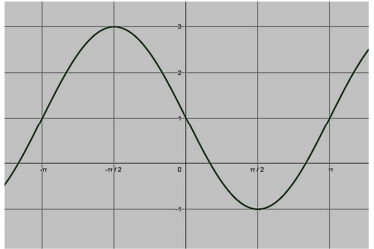
A lei dessa função pode ser dada por
Considere uma função f, de domínio real, dada pela relação:
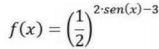
Dessa forma, calcule o máximo valor assumido pela imagem de f.
Considere que sen β = 0,8 e cos θ = 0,5, com θ, β ∈ [0,π/2].
Considerando-se 1,7 como aproximação para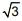 
, o valor mais próximo do valor da expressão 
é igual a
Considere o triângulo retângulo ABC com os catetos AB e AC medindo, respectivamente, 40 e 30. Se M é o ponto médio de AB e N é a intersecção da bissetriz do ângulo ACB com o lado AB, qual é a área do triângulo CNM?
A forma trigonométrica do número complexo z = -√3 + 3i é representada por:
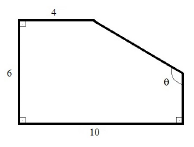
O pentágono apresentado na figura acima possui área igual a
Sabendo‐se que o cos(30) é igual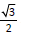 
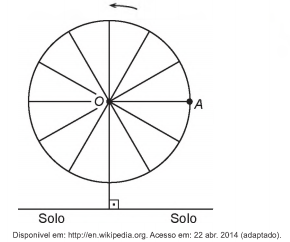
a é correto concluir que o sen2(15) vale
Em 2014 foi inaugurada a maior roda-gigante do mundo, a High Roller, situada em Las Vegas. A figura representa um esboço dessa roda-gigante, no qual o ponto A representa uma de suas cadeiras:
A partir da posição indicada, em que o segmento OA se encontra paralelo ao plano do solo, rotaciona-se a High Roller no sentido anti-horário, em torno do ponto O. Sejam t o ângulo determinado pelo segmento OA em relação à sua posição inicial, e f a função que descreve a altura do ponto A, em relação ao solo, em função de t.
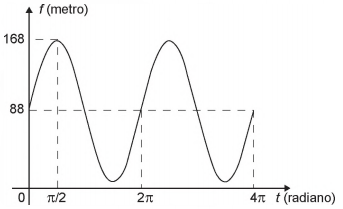
Após duas voltas completas, f tem o seguinte gráfico:
A expressão da função altura é dada por
O retângulo ABCD tem dimensões AB = 2 e BC = 4. Os pontos M e N são médios dos lados BC e CD, respectivamente.
O cosseno do ângulo AMN é igual a
No décimo dia do mês de agosto, a tábua das marés indicou que a maré alta e a maré baixa, na praia do Chapéu Virado, na ilha do Mosqueiro, atingiram 3,5 metros e 0,7 metros de altura, respectivamente. Sabe-se também que a baixa-mar ocorreu ao meio-dia e à meia-noite, enquanto que preamar ocorreu às 06h e às 18h. Considerando que a altura da maré em função do tempo h (t) é dada por um modelo matemático do tipo h(t) - a +b. sen(c.t + d), com a, b, c e d, constantes reais, o número de vezes que a maré atingiu à altura de 2,8 metros, entre 03h e 19h é igual a
A Catedral de São Paulo, em Londres, apresenta um fenômeno interessante chamado “galeria de sussurro”: dois visitantes localizados em pontos diametralmente opostos em relação ao centro podem conversar sussurrando. Isto acontece porque o teto e as paredes da Catedral formam um semi-elipsóide de revolução com focos localizados numa altura razoável. Este fenômeno é conseqüência da seguinte propriedade da elipse:
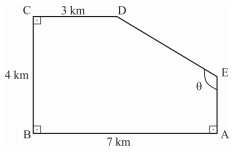
A figura seguinte ilustra um terreno pentagonal no qual será semeado um cultivar que, para desenvolver-se livre de parasitas, receberá a aplicação, para cada hectare, de 0,5 L de um herbicida especial cujo litro custa R$ 60.
Os cinco lados do terreno são retos e formam o pentágono ABCDE antecedente, em que os ângulos nos vértices A, B e C são retos, AB = 7 km, BC = 4 km e CD = 3 km. Sabe-se também que o ângulo no vértice E é θ, em que tg θ = –2 e tg (π – θ) = 2.
Na situação apresentada, o custo do herbicida a ser aplicado no terreno será de
Qual é a área do triângulo a seguir?
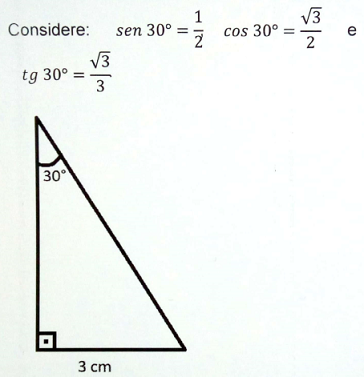
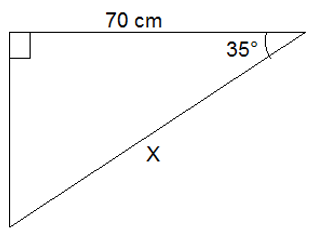
Qual o valor de x? Dado: sen35°=0,57; cos35°=0,82; tan35°=0,7
