O triângulo da figura é denominado triângulo mágico. Nos círculos, escrevem-se os números de 1 a 6, sem repetição, com um número em cada círculo. O objetivo é distribuir os números de forma que as somas dos números em cada lado do triângulo sejam iguais.
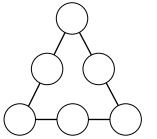
Considere que os números colocados nos vértices do triângulo estejam em progressão aritmética de razão igual a 2.
Nas condições propostas, quais as possíveis soluções para as somas dos números que formam os lados do triângulo?
A figura ilustra uma roda-gigante no exato instante em que a cadeira onde se encontra a pessoa P está no ponto mais alto dessa roda-gigante.
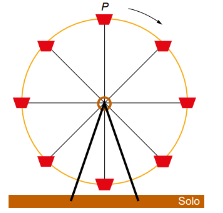
Com o passar do tempo, à medida que a roda-gigante gira, com velocidade angular constante e no sentido horário, a altura da cadeira onde se encontra a pessoa P, em relação ao solo, vai se alterando.
O gráfico que melhor representa a variação dessa altura,em função do tempo, contado a partir do instante em que a cadeira da pessoa P se encontra na posição mais alta da roda-gigante, é
Sejam a, b e c as medidas dos lados de um triângulo retângulo, tendo a como medida da hipotenusa. Esses valores a, b e c são, respectivamente, os diâmetros dos círculos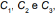 
como apresentados na figura
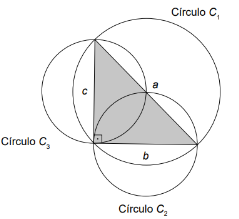
Observe que essa construção assegura, pelo teorema de Pitágoras, que área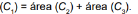 
Um professor de matemática era conhecedor dessa construção e, confraternizando com dois amigos em uma pizzaria onde são vendidas pizzas somente em formato de círculo, lançou um desafio: mesmo sem usar um instrumento de medição, poderia afirmar com certeza se
a área do círculo correspondente à pizza que ele pedisse era maior, igual ou menor do que a soma das áreas das pizzas dos dois amigos. Assim, foram pedidas três pizzas. O professor as dividiu ao meio e formou um triângulo com os diâmetros das pizzas, conforme indicado na figura.
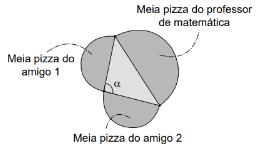
A partir da medida do ângulo a, o professor afirmou que a área de sua pizza é maior do que a soma das áreas das outras duas pizzas.
A área da pizza do professor de matemática é maior do que a soma das áreas das outras duas pizzas, pois
Analisando as vendas de uma empresa, o gerente concluiu que o montante diário arrecadado, em milhar de real,
poderia ser calculado pela expressão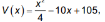 
em que os valores de x representam os dias do mês, variando de 1 a 30.
Um dos fatores para avaliar o desempenho mensal da empresa é verificar qual é o menor montante diário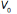 
arrecadado ao longo do mês e classificar o desempenho conforme as categorias apresentadas a seguir, em que as quantidades estão expressas em milhar de real.
No caso analisado, qual seria a classificação do desempenho da empresa?
Numa eleição em que concorreram quatro candidatos e que contou com 963 votantes, o candidato vencedor teve 53 votos a mais do que o segundo classificado, 79 votos a mais do que o terceiro e 105 votos a mais do que o quarto classificado.
A soma do número de votos do vencedor com o número de votos do perdedor é
Em uma feira de ciências, cinco crianças, designadas pelas letras A, B, C, D e E, participarão de um experimento no qual um robô distribuirá três tipos de bala: de morango, de laranja ou de hortelã. A cada nova rodada, somente uma bala será dada pelo robô a cada criança, partindo-se da criança A até a criança E, em ordem alfabética, conforme ilustrado na figura a seguir.
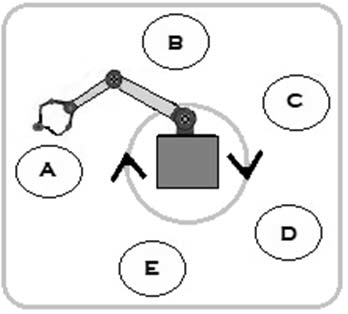
A distribuição das balas seguirá a seguinte rotina, a qual será obedecida também quando se passar de uma rodada para outra: se uma criança receber uma bala de morango, a criança seguinte receberá uma bala de laranja; se uma criança receber uma bala de laranja, a criança seguinte receberá uma bala de hortelã; se uma criança receber uma bala de hortelã, a criança seguinte receberá uma bala de morango.
A partir dessa situação hipotética, julgue os itens seguintes, considerando que a criança A receberá uma bala de morango na primeira rodada.
Na rodada de número 19, a criança D receberá uma bala de hortelã
Ricardo, Antônio, Everaldo e Juliano estão dispostos em torno de uma mesa circular, cada um sentado em um único assento, conforme figura a seguir:
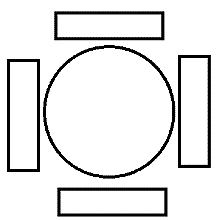
Entre eles, há um procurador, dois desembargadores e um promotor.
Adicionalmente, sabe-se que:
- Os dois desembargadores estão sentados um ao lado do outro.
- Antônio é procurador e está ao lado de Ricardo.
- Juliano é desembargador e Antônio está sentado à sua esquerda.
Considerando que cada profissional exerce uma única função, é correto afirmar que:
João e Maria são amigos há 15 anos. Curiosamente, quando se conheceram, 18 vezes a idade de João menos o quadrado dessa mesma idade era igual a 80. Os mesmos dados valiam, naquela ocasião, para a idade de Maria.
Tendo em vista o exposto, a soma das idades atuais de João e Maria vale
As idades das quatro primas Fernanda, Gláucia, Helena e Íris são 13, 18, 22 e 24, embora não necessariamente nessa ordem.
Fernanda é mais nova do que Helena. A soma das idades de Íris e Fernanda é divisível por 5. A soma das idades de Íris e Helena também é divisível por 5.
A soma das idades de Fernanda e Gláucia é
Em uma feira de ciências, cinco crianças, designadas pelas letras A, B, C, D e E, participarão de um experimento no qual um robô distribuirá três tipos de bala: de morango, de laranja ou de hortelã. A cada nova rodada, somente uma bala será dada pelo robô a cada criança, partindo-se da criança A até a criança E, em ordem alfabética, conforme ilustrado na figura a seguir.
A distribuição das balas seguirá a seguinte rotina, a qual será obedecida também quando se passar de uma rodada para outra: se uma criança receber uma bala de morango, a criança seguinte receberá uma bala de laranja; se uma criança receber uma bala de laranja, a criança seguinte receberá uma bala de hortelã; se uma criança receber uma bala de hortelã, a criança seguinte receberá uma bala de morango.
A partir dessa situação hipotética, julgue os itens seguintes, considerando que a criança A receberá uma bala de morango na primeira rodada.
Ao final da sétima rodada, a criança A terá recebido, pelo menos, três balas de morango
Considere a seguinte equação:
95 . 32/814 O resultado dessa equação é:
As amigas Ana, Bruna, Carla e Denise vão a uma festa e cada uma tem um vestido. Como querem usar um vestido diferente, decidiram que cada uma irá usar o vestido de uma das outras. O número de maneiras distintas de fazerem isso é igual a
Ana, André e Abel são trigêmeos e têm um irmão 5 anos mais novo.
Das alternativas a seguir, a única que poderia ser a soma das idades dos 4 irmãos é
Em um jogo de adivinhação Maria escolhe três cores em sequência, podendo repetir cores. As cores que Maria pode escolher são Marrom, Verde e Azul. Maria então pergunta a Antônio que cores ela escolheu. Quando Antônio fala três cores numa dada ordem da sequência, Maria responde quantas cores estão certas e na posição certa da sequência e quantas cores estão certas, mas na posição errada.
Antônio fez duas tentativas.
- Antônio: As cores são Azul, Marrom e Marrom, nesta ordem.
- Maria: Você acertou duas cores, mas estão na posição errada.
- Antônio: As cores são Marrom, Verde e Verde.
- Maria: Você acertou duas cores e estão na posição certa.
Dadas as informações acima, o número de sequências de cores que podem ter sido escolhidas por Maria é:
Um tesouro foi escondido em uma região plana e o mapa que permite localizar esse tesouro é o seguinte: “A partir da torre de transmissão de energia, ande 30 passos a leste; depois, 10 passos a norte e 25 passos a oeste. Caminhe 10 passos a norte e, em seguida, 10 passos a leste e aí estará o tesouro”. A quantos passos, em linha reta, está o tesouro da torre de transmissão de energia? (Admita que todos os passos têm o mesmo comprimento e despreze as dimensões da torre de transmissão de energia).
