Uma pessoa comprou um ingresso para o cinema em cuja entrada está afixado um mapa com a representação bidimensional do posicionamento das poltronas, conforme a figura. Essa pessoa, após consultar o mapa, começou a subir uma das escadas e parou na posição indicada pela estrela, direcionada para o norte. Ela conferiu seu bilhete e observou que, para encontrar sua poltrona, deveria partir do ponto onde estava, continuar subindo a escada na direção norte por mais quatro fileiras e olhar à sua direita, e sua poltrona será a terceira.
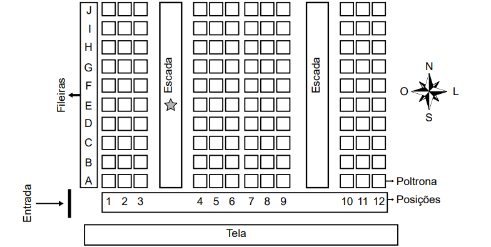
Nesse cinema, as poltronas são identificadas por uma letra, que indica a fileira, e um número, que fornece a posição da poltrona na fileira, respectivamente.
A poltrona dessa pessoa é a identificada por
As características culturais variam de povo para povo. Há notícias de um povo que possuía formas de contar diferentes das nossas, como indicado no quadrinho a seguir
Segundo o padrão de contagem indicado na figura, as representações dos numerais cinco e sete, nessa cultura, devem ser, respectivamente,
Uma empresa produz tintas de cor cinza, em dois modelos. No modelo 1, ela usa a proporção de 7 colheres de tinta preta para 3 colheres de tinta branca. No modelo 2, a proporção é de 2 colheres de tinta preta para 3 colheres de tinta branca. A empresa usará 1.100 galões de tinta preta e 900 galões de tinta branca na produção dos dois modelos.
Nesse caso, o total de galões do modelo 1 que serão produzidos é igual a:
Em certo reino distante, a moeda nacional é o irreal. Há apenas notas de 5 e de 6 irreais. Em visita ao reino, dr. Blanc levou uma bolsa com 500 notas de 5 irreais e 500 notas de 6 irreais. Ele comprou por 1.214 irreais uma escultura local e pagou essa quantia usando o maior número de notas possível.
O total de notas usadas pelo dr. Blanc foi de:
No primeiro dia de agosto, foram registradas 180 reclamações em um órgão de defesa do consumidor. No segundo dia, foram registradas 184 reclamações.
Supondo-se que há reclamações todos os dias e que cada dia tenha 4 reclamações a mais do que o dia anterior, durante todos os 31 dias do mês de agosto, o total de reclamações registradas será igual a
Dora começa a ler um livro de 174 páginas em um domingo. Ela lê 5 páginas por dia exceto aos domingos, quando lê 16 páginas. Para terminar a leitura do livro, que foi feita em dias consecutivos, Dora precisou exatamente de
Estudantes trabalhando com robótica criaram uma “torneira inteligente” que automatiza sua abertura e seu fechamento durante a limpeza das mãos. A tecnologia funciona da seguinte forma: ao se colocarem as mãos sob a torneira, ela libera água durante 3 segundos para
que a pessoa possa molhá-las. Em seguida, interrompe o fornecimento de água por 5 segundos, enquanto a pessoa ensaboa suas mãos, e finaliza o ciclo liberando água para o enxágue por mais 3 segundos. Considere o tempo ( t ), em segundo, contado a partir do instante em que se inicia o ciclo. A vazão de água nessa torneira é constante.
Um esboço de gráfico que descreve o volume de água acumulado, em litro, liberado por essa torneira durante um ciclo de lavagem das mãos, em função do tempo (t ), em segundo, é
Entre maratonistas, um parâmetro utilizado é o de economia de corrida (EC). O valor desse parâmetro é calculado pela razão entre o consumo de oxigênio, em mililitro (mL) por minuto (min), e a massa, em quilograma (kg), do atleta correndo a uma velocidade constante.
Disponível em: www.treinamentoonline.com.br. Acesso em: 23 out. 2019 (adaptado).
Um maratonista, visando melhorar sua performance, auxiliado por um médico, mensura o seu consumo de oxigênio por minuto a velocidade constante. Com base nesse consumo e na massa do atleta, o médico calcula o EC do atleta. A unidade de medida da grandeza descrita pelo parâmetro EC é
Em uma turma de 30 alunos, 18 preferem matemática, 12 preferem português e 6 não gostam de nenhuma das duas disciplinas.
A quantidade de alunos, que gostam tanto de matemática como de português, é de:
Ana, Bia, Carla e Diana têm 20 anéis. Ana é quem tem mais anéis, Bia tem um anel a menos do que Ana, Carla é quem tem menos anéis e Diana tem um anel a mais do que Carla. Sabendo-se que todas têm pelo menos 3 anéis, é correto afirmar:
Se a ≠ 0 e b ≠ 0, então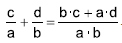 
.
Ou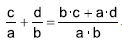 
ou a e b são números complexos.
Sabendo-se que a, b, c, d são números racionais e k
é um número real diferente de zero, é necessariamente
verdade que
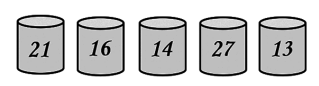
Em cada uma da slatas da Figura acima há apenas lápis e borrachas. O número escrito em cada uma dessas latas indica a quantidade total desses objetos nela contidos. Uma dessas latas foi retidada e, considerando-se apenas as quatro latas restantes, o número total de lápis passou a ser o triplo do número total de borrachas.
Considerando-se apenas as quatro latas restantes, o número total de lápis existente nelas é igual a
As irmãs N, T e S apostaram uma corrida. Elas têm uma peculiaridade: N nunca mente; T às vezes mente; S sempre mente.
• Quem ficou em 1° lugar disse: “S ficou em 2° lugar”.
• Quem ficou em 2° lugar disse: “Eu sou T”.
• Quem ficou em 3° lugar disse: “N ficou em 2° lugar”.
Nessa corrida, tem-se como 1° lugar, 2° lugar e 3° lugar, respectivamente,
Em uma pequena cidade há três agências de um banco, nomeadas A1, A2 e A3. Técnicos desse banco estão analisando um mapa para escolher o local para abrir uma quarta agência. A Figura a seguir é um esboço desse mapa, que contém também as seguintes informações:
• Para ir de A1 para A2, passando por A3, percorrem-se 7,8 km;
• Para ir de A3 para A1, passando por A2, percorrem-se 9,9 km;
• Para ir de A2 para A3, passando por A1, percorrem-se 11,3 km.
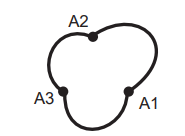
Uma pessoa decidiu ir de A1 para A3, sem passar por A2, depois ir de A3 para A2, sem passar por A1 e, finalmente, ir de A2 para A1, sem passar por A3.
Com base na Figura e nas informações do mapa, essa pessoa percorreu, ao todo, uma distância, em km, igual a
Considere que em certo quartel haja sete soldados e cinco cabos disponíveis.
A quantidade de equipes diferentes de seis pessoas, com três cabos e três soldados, que podem ser formadas a partir dos militares disponíveis nesse quartel é igual a
