Uma partida de futebol society foi realizada entre 2 times: o time A era composto de 1 goleiro, 2 zagueiros, 2 meio-campistas e 2 atacantes; e o time B era composto de 1 goleiro, 2 zagueiros, 3 meio-campistas e 1 atacante. No primeiro tempo, o juiz expulsou um jogador de cada time e, no final do segundo tempo, expulsou apenas um jogador do time B.
Com base nessa situação hipotética, é correto afirmar que a probabilidade de o juiz ter expulsado pelo menos um meio-campista é de
Sabendo que o sistema solar é composto por 8 planetas (Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano e Netuno), julgue o item.
Escolhendo-se um dos planetas do sistema solar ao acaso, a probabilidade de o planeta começar e terminar com uma consoante é inferior a 25%.
Sabe‐se que, a cada 10 pênaltis marcados a favor de um time de futebol, 6 são cobrados por Bárbara e 4 por Débora. A probabilidade de um pênalti ser convertido por Bárbara é de 90% e a de ser convertido por Débora, de 80%.
Com base nessa situação hipotética, julgue o item.
A probabilidade de um pênalti ser cobrado e convertido por Bárbara é de 54%.
Sabe‐se que, a cada 10 pênaltis marcados a favor de um time de futebol, 6 são cobrados por Bárbara e 4 por Débora. A probabilidade de um pênalti ser convertido por Bárbara é de 90% e a de ser convertido por Débora, de 80%.
Com base nessa situação hipotética, julgue o item.
Se um pênalti foi convertido, então a probabilidade de ele ter sido cobrado por Bárbara é superior a 60%.
Em uma campanha promocional de uma loja, um cliente gira uma roleta, conforme a apresentada no esquema, almejando obter um desconto sobre o valor total de sua compra. O resultado é o que está marcado na região apontada pela seta, sendo que todas as regiões
são congruentes. Além disso, um dispositivo impede que a seta venha a apontar exatamente para a linha de fronteira entre duas regiões adjacentes. Um cliente realiza uma compra e gira a roleta, torcendo para obter o desconto máximo.
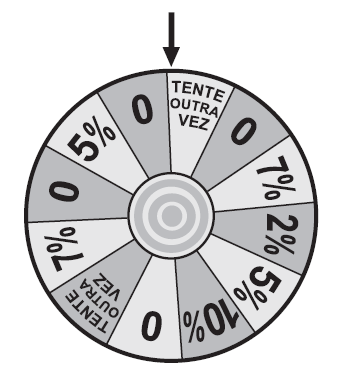
A probabilidade, em porcentagem, de esse cliente ganhar o desconto máximo com um único giro da roleta é melhor aproximada por
Os professores João, Carlos e Luis ministrarão um curso de primeiros socorros em que serão ensinados os seguintes procedimentos.
I fazer massagem cardíaca
II desengasgar
III estancar sangramentos
IV amenizar queimaduras
V desafogar
VI cuidar de fraturas
Cada professor ensinará exatamente dois procedimentos, e o mesmo professor que ensinar o procedimento desafogar ensinará também o procedimento desengasgar.
Considerando essa situação hipotética, julgue o próximo item.
Selecionando-se ao acaso o professor que ensinará o procedimento fazer massagem cardíaca, a probabilidade de Luis ser o escolhido é maior do que 40%.
Texto 1A6-I
Cinco pessoas (Arnaldo, Bernardo, Cláudio, Diógenes e Ernesto), suspeitas de determinada contravenção, são chamadas para acareação por uma autoridade policial. Exatamente dois deles são culpados, e as seguintes declarações foram feitas durante o depoimento:
I. Arnaldo disse que os culpados não foram Ernesto nem Bernardo;
II. Bernardo disse que os culpados não foram Arnaldo nem Cláudio;
III. Cláudio disse que os culpados não foram Bernardo nem Diógenes.
No texto 1A6-I, se 3 pessoas forem aleatoriamente escolhidas entre os 5 suspeitos, então a probabilidade de os dois culpados serem escolhidos será igual a
Considere que em um plantão estejam trabalhando 10 bombeiros, 4 mulheres e 6 homens, e que 3 dessas pessoas devam ser escolhidas ao acaso para atender a uma ocorrência. Nessa situação, a probabilidade de que sejam escolhidas para o atendimento exatamente 2 mulheres é de
Considere os seguintes conjuntos:

e, assim, sucessivamente.
Com base nessas informações, julgue o item que se segue:
Escolhendo-se aleatoriamente um integrante do conjunto P, a probabilidade de ele ter entre dois e três anos de experiência no exercício do cargo é dada por n(P2 — P3)/n(P3), em que n(X) indica o número de elementos do conjunto X e P2 — P3 é o conjunto formado pelos indivíduos que estão em P2, mas não estão em P3
Sabe‐se que, a cada 10 pênaltis marcados a favor de um time de futebol, 6 são cobrados por Bárbara e 4 por Débora. A probabilidade de um pênalti ser convertido por Bárbara é de 90% e a de ser convertido por Débora, de 80%.
Com base nessa situação hipotética, julgue o item.
A probabilidade de esse time desperdiçar um pênalti é maior que 15%.
Um apostador deve escolher uma entre cinco moedas ao acaso e lançá-la sobre umamesa, tentando acertar qual resultado (cara ou coroa) sairá na face superior da moeda.
Suponha que as cinco moedas que ele pode escolher sejam diferentes:
• duas delas têm “cara” nas duas faces;
• uma delas tem “coroa” nas duas faces;
• duas delas são normais (cara em uma face e coroa na outra).
Nesse jogo, qual é a probabilidade de o apostador obter uma face "cara" no lado superior damoeda lançada por ele?
Para um docente estrangeiro trabalhar no Brasil, ele necessita validar o seu diploma junto ao Ministério da Educação. Num determinado ano, somente para estrangeiros que trabalharão em universidades dos estados de São Paulo e Rio de Janeiro, foram validados os diplomas de 402 docentes estrangeiros. Na tabela, está representada a distribuição desses docentes estrangeiros, por países de origem, para cada um dos dois estados.

A probabilidade de se escolher, aleatoriamente, um docente espanhol, sabendo-se que ele trabalha em uma universidade do estado de São Paulo é
Considerando dois eventos aleatórios A e B, tais que P(A|B) = 1/3, P(B|A) = 0,5 e P(A B) = 0,8, julgue os seguinte item.
P(A) > P(B).
Um aluno da EsPCEx tem a probabilidade de 60% de acertar um problema de Matemática ao tentar resolvê-lo. Numa prova de Matemática com 5 problemas, qual a probabilidade desse aluno acertar ao menos um dos 5 problemas?
Suponha que uma equipe de corrida de automóveis disponha de cinco tipos de pneu (I, II, III, IV, V), em que o fator de eficiência climática EC (índice que fornece o comportamento do pneu em uso, dependendo do clima) é apresentado:
• EC do pneu I: com chuva 6, sem chuva 3;
• EC do pneu II: com chuva 7, sem chuva −4;
• EC do pneu III: com chuva −2, sem chuva 10;
• EC do pneu IV: com chuva 2, sem chuva 8;
• EC do pneu V: com chuva −6, sem chuva 7.
O coeficiente de rendimento climático (CRC) de um pneu é calculado como a soma dos produtos dos fatores de EC, com ou sem chuva, pelas correspondentes probabilidades de se ter tais condições climáticas: ele é utilizado para determinar qual pneu deve ser selecionado para uma dada corrida, escolhendo-se o pneu que apresentar o maior CRC naquele dia. No dia de certa corrida, a probabilidade de chover era de 70% e o chefe da equipe calculou o CRC de cada um dos cinco tipos de pneu.
O pneu escolhido foi

