Pedro lançou dois dados não viciados em sequência com o intuito de descobrir algumas probabilidades a respeito desses lançamentos. Nos lançamentos de Pedro, qual é a probabilidade de se obter 3 no primeiro lançamento e 6 no segundo lançamento?
um grupo de pessoas, o número de homens é igual ao número de mulheres. Selecionam-se então dos homens e das mulheres e forma-se um novo grupo.
Nesse novo grupo, em relação ao total de pessoas, as mulheres representam
Numa caixa há seis bolas numeradas de 1 a 6. Considere todas as bolas iguais em tamanho, cor e densidade. O que as difere são apenas os números. Retiram-se duas bolas ao acaso desta caixa simultaneamente. Assinale a alternativa que apresenta qual a probabilidade de retirar essas duas bolas com números cuja soma deles seja um resultado múltiplo de 3.
Foi modelado que o espalhamento de uma notícia em uma população — entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo — é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.
Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue o item a seguir.
Se, em determinado instante, o espalhamento de uma notícia é igual a 16% por unidade de tempo, então, nesse instante, mais de 75% da população ainda desconhece a notícia.
Um hospital possui duas alas de UTI, totalizando 210 leitos. A primeira destina 25% dos leitos a pacientes infectados pela COVID-19; e a segunda, 50% dos leitos a pacientes com essa doença. Sabe-se que o número total de leitos destinados a pacientes com COVID-19, nas
duas UTIs, representa 40% do total de leitos de UTI no hospital. Desse modo, o número de leitos destinados a esses pacientes, na UTI com menor capacidade, é:
Uma pesquisa realizada numa loja que vende computadores mostrou que a probabilidade de uma pessoa ficar satisfeita com a compra de um determinado produto é de 95%. A probabilidade de três pessoas ficarem insatisfeitas após a compra desse produto é de:
Considerando que A e B sejam eventos aleatórios independentes e que P(A) = 0,8 e P(B) = 0,2, julgue o próximo item.
A tabela a seguir fornece, por sexo e por cargo pretendido, a quantidade total de candidatos inscritos em um concurso público.
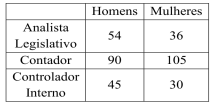
Escolhendo-se ao acaso um dos candidatos inscritos nesse concurso, a probabilidade de a pessoa escolhida ser mulher ou pretender um cargo de contador é de:
Os professores João, Carlos e Luis ministrarão um curso de primeiros socorros em que serão ensinados os seguintes procedimentos.
I fazer massagem cardíaca
II desengasgar
III estancar sangramentos
IV amenizar queimaduras
V desafogar
VI cuidar de fraturas
Cada professor ensinará exatamente dois procedimentos, e o mesmo professor que ensinar o procedimento desafogar ensinará também o procedimento desengasgar.
Considerando essa situação hipotética, julgue o próximo item.
Se Carlos ensinar o procedimento cuidar de fraturas, então, selecionando-se ao acaso os professores que ensinarão os outros procedimentos, a chance de que João ensine o procedimento desafogar é maior do que 45%.
Sabendo que o sistema solar é composto por 8 planetas (Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano e Netuno), julgue o item.
Suponha-se que uma urna contenha 8 bolinhas e que, em cada uma, esteja escrito o nome de um planeta do sistema solar. Nesse caso, extraindo-se duas bolinhas sucessivamente ao acaso e com reposição, a probabilidade de que em nenhuma delas esteja escrito “Terra” é igual a 75%.
As informações cadastrais de todos os funcionários de uma determinada empresa de logística são sumarizadas em relatórios emitidos mensalmente. O gráfico representa o diagrama de caixa (box-plot) com a distribuição do número de salários mínimos de todos os funcionários dessa empresa em um certo mês.

A partir desses dados, considere que três funcionários sejam selecionados aleatoriamente. Qual a probabilidade aproximada (*) de que pelo menos um deles receba mais do que sete salários mínimos? (*)[Considerar duas casas decimais.]
Considere que, quando Carlos, agente de pesquisas por telefone, realiza uma chamada telefônica, a chance de que a sua chamada não seja atendida seja de 20% e que, se a chamada for atendida, a chance de que ele obtenha respostas verdadeiras seja de 60%. Nessa situação, a probabilidade de Carlos obter respostas verdadeiras em uma dada chamada telefônica é igual a
Uma primeira urna possui uma bola branca e duas pretas. Uma segunda urna possui duas bolas brancas e uma preta. Uma terceira urna, por sua vez, possui uma bola branca e uma preta. Uma pessoa vendada retira uma bola da primeira urna e a coloca na segunda. Em seguida, retira uma bola da segunda urna e a coloca na terceira. Por fim, retira uma bola da terceira urna.
Sabendo que todas a bolas são idênticas em forma e peso, quantas possibilidades há de que a bola retirada da terceira urna seja preta?
Considerando que A e B sejam eventos aleatórios independentes e que P(A) = 0,8 e P(B) = 0,2, julgue o próximo item.
P(A B) = 0
Uma casa lotérica oferece cinco opções de jogos. Em cada opção, o apostador escolhe um grupo de K números distintos em um cartão que contém um total de N números disponíveis, gerando, dessa forma, um total de C combinações possíveis para se fazer a marcação do cartão. Ganha o prêmio o cartão que apresentar os K números sorteados. Os valores desses jogos variam de R$ 1,00 a R$ 2,00, conforme descrito no quadro.

Um apostador dispõe de R$ 2,00 para gastar em uma das cinco opções de jogos disponíveis.
Segundo o valor disponível para ser gasto, o jogo que oferece ao apostador maiorprobabilidade de ganhar prêmio é o

