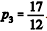Considere as igualdades abaixo.
I. √0,25 = 0,5
II. 0,3 : 0,1 = 0,3 I
II. √50 = 5√2
São corretas as igualdades:
Qual é o resultado de 3 + 6 . 5 – 8 : 4 ?
Na moldura abaixo há as medidas recomendadas para confecção de uma escada, em que as medidas dos pisos (patamares horizontais) podem variar de 25cm a 35cm e dos espelhos (faces verticais entre um piso e outro) podem medir entre 14cm e 18cm. No lado direito da moldura há o esboço de um projeto de escada, apenas com início e fim, que tem a mesma quantidade de pisos e espelhos uniformes e devem adotar as medidas recomendadas.
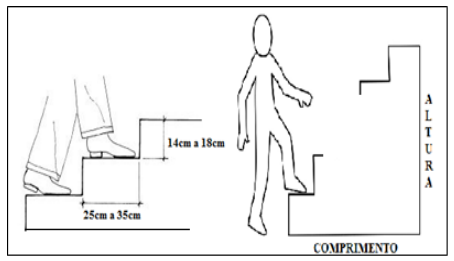
Sabendo-se que 1m equivale a 100cm e que a soma do comprimento e da altura da escada da direita deve variar entre 3m12cm e 4m24cm, então a quantidade de pisos dessa escada deve ser igual a
Cada j = 0, 1, …, 11 representa um mês do ano de 2017, isto é, j = 0 = janeiro, j = 1 = fevereiro, e assim sucessivamente. Se o mês j tem d dias, então j + 1/d representa o dia 1.º do mês j; j + 2/d representa o dia 2 do mês j, e assim sucessivamente, j + d/d = j + 1 representa o dia d do mês j. Dessa forma, cada dia do ano de 2017 pode ser representado por um número x do intervalo [0, 12]. Considere que, nessa representação, em cada dia x do ano de 2017, a porcentagem de água acumulada em relação à capacidade máxima do reservatório de determinada represa seja expressa pelo valor da função f(x) = x2 - 10x + 60.
A partir dessas informações, julgue o item que se segue.
A diferença entre os percentuais de água contida na represa em 31/12/2017 e 1.º/1/2017 é superior a 20%.
A respeito de história da matemática, julgue o item subsequente.
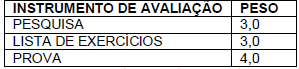
Os babilônicos possuíam um método próprio para o cálculo da raiz quadrada de um número, utilizando aproximações sucessivas. Para determinar o valor aproximado de
se estimava, primeiramente, um valor p1 para essa raiz e calculava-se o quociente 
. Com esses dois números calculava-se um novo valor p2, a média aritmética de p1 e q1, isto é, 
. Repetindo esse processo sucessivamente, obtinha-se uma aproximação da raiz quadrada. No método babilônico, se a estimativa inicial para 
for p1 = 1, então a terceira aproximação de será 
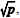
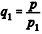
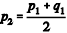
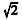
Em uma escola, a nota final do bimestre na disciplina de matemática é calculada pela média das notas obtidas em cada instrumento de avaliação oferecido, considerando seus pesos. Em uma determinada ocasião, o professor de matemática ofereceu três instrumentos de avaliação às suas turmas, conforme segue na tabela abaixo:
Supondo que um aluno tenha obtido as notas 7, 7 e 5 na pesquisa, lista de exercícios e prova, respectivamente, a nota final obtida no bimestre pelo aluno é:
Se 3 operários constroem 3 paredes em 3 dias, então o número de dias que 50 operários construirão 50 paredes é de:
Resolva as operações e em seguida, assinale a alternativa que apresenta o resultado CORRETO.
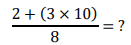
Leia as afirmativas a seguir:
I. Paganini comprou um produto importado por 51 euros. Considerando que na época o valor do Euro era de R$ 3,60, podemos afirmar que Paganini gastou mais de R$ 200.
II. Uma dúzia corresponde a 12% de 24 unidades.
Marque a alternativa CORRETA:
Um funcionário público deixa seu veículo em certo estacionamento, sempre das 8h30min às 12h30min, durante 5 dias da semana. Nesse estacionamento, diariamente, são cobrados R$ 1,50 pela primeira hora e R$ 0,75 por hora sucessiva. Com base nos dados apresentados, pode-se estimar que o gasto semanal dessa pessoa, com o estacionamento, é:
Foram realizadas algumas pesquisas nos mercados sobre o preço do feijão, sendo obtido os seguintes valores: R$ 2,30; R$ 2,57; R$ 3,50; R$ 4,10; R$ 2,15; R$ 3,68 e R$ 4,23. Com base nesses valores, a variação de preço foi de:
O valor numérico da expressão algébrica quando x= 2 e y =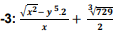 
é:
O maior valor monetário, em reais, de três notas de valores diferentes e três moedas de valores diferentes é igual a
José possuía a quantia de R$70,00. Gastou 1⁄7 desse montante na compra de medicamentos, 2⁄5 na compra de um livro e 3⁄10 na compra de um CD. Com quanto ele ainda ficou?
Eduardo paga mensalmente um boleto bancário de R$ 372,00. Após o vencimento é cobrado uma multa de R$7,50 e a cada dia de atraso uma multa diária de R$ 0,12. No mês de maio Eduardo só conseguiu pagar esse boleto 4 dias depois do vencimento. Qual é a quantia total que ele deverá pagar?
