Sejam x um ângulo qualquer, em radianos, e i a unidade imaginária. O determinante da matriz é igual a
Suponha que o número diário (X) de transações bancárias registradas em determinada conta bancária se distribua conforme uma distribuição de Poisson. Com respeito ao total semanal de transações bancárias registradas nessa conta bancária, denotada como Y= X1 + X2 + X3 + X4 + X5 em que {X1,… , X5} representa uma amostra aleatória simples retirada de uma distribuição de Poisson com média igual a 5 transações por dia, julgue o seguinte item
P(Y=0) = P(X1=0) + P(X2=0) + P(X3=0) + P(X4=0) + P(X5=0) = 5 X e-5
Dado o sistema linear os valores do número real a , tais que o sistema linear acima tenha solução, pertencem ao conjunto
Se M é uma matriz quadrada de ordem 2 e N uma matriz quadrada de ordem 3, tal que 2 ∙ det M + det N = –1, então o valor de det (4M) + det (2N) é:
Num sistema de coordenadas cartesianas ortogonais, verificou-se que os pontos A(a,1,a), B(2a, 1, a), C(b, a, a) distintos são colineares. Além disso o sistema:
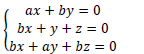
possui solução não trivial. Logo:
Se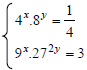 
, qual o valor de x + y?
O estudo das matrizes tem muitas aplicações na computação gráfica. É através de operações com matrizes que um programa gráfico altera a posição dos pontos que compõem uma imagem, fazendo-a girar, mudar de posição ou de escala. Na computação grafia, essas operações recebem o nome de transformações geométricas. Por exemplo, uma rotação de 0 graus de um ponto P = (x ,y ), em torno da origem no sentido anti-horário é feita a partir do produto da matriz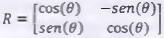 
de rotação com a matriz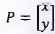 
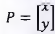, que resulta em uma matriz 
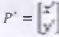, a qual indica a nova posição do ponto após a rotação: P¹ = R . P
A nova posição do ponto P = (1,2) apos uma rotação de 90 graus no sentido anti-horário, tomo da origem, é:
Os vetores (1,2,5), (3,2,1) e (9,2,-11) no espaço vetorial R³ geram um subespaço vetorial ao qual pertence o vetor
Se P é uma matriz 2x2 tal que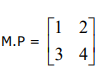 
, então, o determinante da matriz P é igual a
Considerando que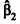 
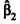
representa o estimador de mínimos quadrados ordinários de β2, a variância de 
é igual a 0,8.
No espaço vetorial
2, B1 = n{(1,1),(2,1)} e B2 = {u,v} são bases tais que a matriz 
é a matriz de mudança da base B1 para B2.
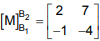
O produto interno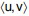 
é igual a
Se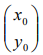 
é solução da equação matricial 
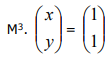, então, o valor da soma x0 + y0 é igual a
Como o determinante de M é não nulo, a matriz M é invertível. Se sua inversa é da forma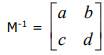 
, então, o resultado da expressão numérica 5a + 4b + 3c + 2d é
Sistemas lineares homogêneos possuem, pelo menos, uma solução e, portanto, nunca serão considerados impossíveis. O sistema linear dado abaixo possui infinitas soluções.
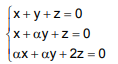
Qual o maior valor possível para α?
A distância entre os pontos A(-3, 4) e B(2, -1) é igual a :
