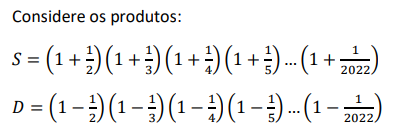Para a pintura externa de um prédio foram contratados pintores no regime de trabalho de 6 horas por dia.
Sabe-se que 5 desses pintores realizam a pintura em exatamente 10 dias inteiros de trabalho.
Se apenas 3 pintores forem contratados no mesmo regime de trabalho, o tempo que levarão para concluir a pintura é de
No futebol, para a cobrança de uma falta, a barreira deve ficar a 10 jardas da bola segundo a regra oficial. Sabe-se que 1 jarda é
equivalente a 3 pés, que 1 pé equivale a 12 polegadas e que uma polegada é equivalente a 2,54 cm.
Em metros, a distância da bola à barreira deve ser oficialmente igual a
Um número inteiro positivo N, de 2 algarismos, é tal que exatamente 3 das 4 afirmações a seguir são verdadeiras:
- N é um número par;
- N é um número primo;
- N é um múltiplo de 3;
- um dos algarismos de N é 5.
O algarismo das unidades de N é
Em um campeonato de futebol de turno único com 10 times, cada time joga uma única vez com cada um dos outros 9. Cada vitória vale 3 pontos, cada empate vale 1 ponto e cada derrota vale 0 (zero) ponto. Ao final, 3 times acabaram empatados (mesmo número total de pontos) em primeiro lugar.
Assinale a opção que indica o número máximo de pontos que cada um desses 3 times fez.
Ana e Bia são crianças e possuem moedas de 1 real em seus cofrinhos. Certo dia, Ana deu para Bia a mesma quantidade de moedas que Bia tinha e, em seguida, Bia deu para Ana a mesma quantidade de moedas que Ana tinha.
Após essa operação, as duas crianças ficaram com 32 moedas cada uma.Bia tinha, inicialmente,
De um grupo de 1000 soldados, uma parte foi dividida em grupos de 15 soldados e o restante foi dividido em 5 grupos de 17 soldados.
O número de grupos de 15 soldados é
No retângulo ABCD da figura abaixo, AB = 600 m e BC = 400 m. O retângulo está em um plano horizontal dividido em quadrados
iguais. Pedro e Mário estão no ponto A e pretendem atingir o ponto P, cada um por um caminho, sobre as linhas destacadas do
desenho. Pedro inicia seu percurso na direção do ponto D e Mário inicia seu percurso na direção do ponto B. Ambos chegam ao ponto P.
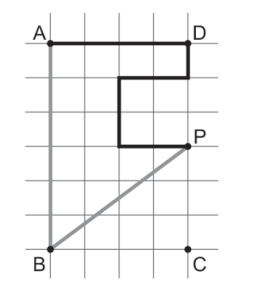
É correto afirmar que
Considere o triângulo retângulo ABC cujos lados medem:
AB = 12, AC = 5 e BC = 13.
Seja D um ponto sobre o lado BC tal que os triângulos ABD e ACD tenham perímetros iguais.
A área do triângulo ABD é
Valter entrou em uma loja e ficou interessado em quatro produtos: A, B, C e D. Os preços unitários em reais estão na tabela abaixo:
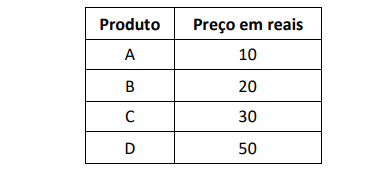
Valter gastou 60 reais comprando alguns desses produtos.
O número de maneiras diferentes em que Valter pode ter efetuado sua compra é
Amélia e Deise estudam na mesma turma de uma escola e resolveram juntas 40% dos exercícios de um “dever de casa”. Depois, cada uma resolveu sozinha os 60% restantes. Após a correção, verificou-se que Amélia acertou 75% dos exercícios que ela fez sozinha e 81% do total. Deise acertou 85% dos exercícios que fez sozinha.
Do total de exercícios, a porcentagem que Deise acertou foi
Seja M o menor número inteiro, maior do que 2, que, dividido por 3, por 5, ou por 7, deixa sempre resto 2.
A soma dos algarismos de M é
Isabel comprou, em um supermercado, 3 kg de arroz e 4 kg de feijão, pagando o total de R$ 63,00. Na semana seguinte, no mesmo supermercado e com os mesmos preços, ela comprou 5 kg de arroz e 2 kg de feijão, pagando R$ 56,00.
Nesse supermercado, para comprar 1 kg de arroz e 1 kg de feijão, com os mesmos preços, Isabel deve pagar
Uma turbina de geração de energia foi ligada ao meio-dia do dia 01 de junho. Após 800 horas de trabalho contínuo, a turbina foi desligada para manutenção.
A turbina foi desligada para a primeira manutenção às
Em uma caixa há várias bolas, cada uma de uma cor. As cores das bolas são: vermelho, azul, verde e rosa. Há, pelo menos, uma
bola de cada cor.Um terço das bolas são vermelhas, um quinto são azuis e 10 bolas são verdes.
O número mínimo de bolas rosas na caixa é