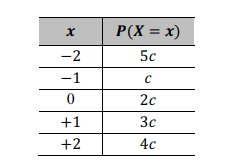
Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A moda de X é igual a zero.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
Em relação aos eventos V ≥0 e W ≥0, é correto afirmar que a probabilidade condicional P(V ≥ 0 I W ≥ 0 ) deve ser superior a 0,3.

Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A mediana de X é igual ou superior a 1.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
A probabilidade de ocorrência simultânea dos eventos V < 0 e W < 0 é igual a 0,21.

Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A média de X é igual a zero.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
O primeiro quartil da variável V é inferior a zero.

Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
X segue uma distribuição contínua, pois c é uma constante real positiva.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
Considerando-se que as médias de V e W sejam iguais a 1 e que o coeficiente de variação de V seja igual ao dobro do coeficiente de variação de W , é correto concluir que a variância de V deve ser igual ao dobro da variância de W.

Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
P (X = 1) = 0,2
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
Se o desvio padrão de V for igual a 3 e se o desvio padrão de W for igual a 4, então o desvio padrão da diferença V - W será igual a 5.

