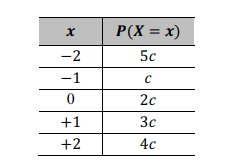
Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A moda de X é igual a zero.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
Em relação aos eventos V ≥0 e W ≥0, é correto afirmar que a probabilidade condicional P(V ≥ 0 I W ≥ 0 ) deve ser superior a 0,3.
Considerando que o desvio padrão amostral de uma amostra aleatória simples retirada de uma população normal seja denotado por Sn , julgue o próximo item
Se n = 100, então a esperança matemática do estimador S100 é igual ao desvio padrão populacional.
No que se refere a vetores autorregressivos, julgue o item que se segue.
Uma série temporal é considerada estacionária se suas médias e variâncias permanecerem constantes ao longo do tempo e se ela não exibir tendências ou sazonalidade.
Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A mediana de X é igual ou superior a 1.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
A probabilidade de ocorrência simultânea dos eventos V < 0 e W < 0 é igual a 0,21.
Supondo que os valores 3, 0, 0, 1, 4 constituam uma realização de uma amostra aleatória simples de tamanho n igual a 5 retirada de uma população com função de probabilidade
denota o parâmetro a ser estimado e x ∈ {0, 1, 2, … }, julgue o seguinte item.
A estimativa de máxima verossimilhança da probabilidade P (X = 0) é igual à frequência relativa de zeros na amostra, ou seja, 2/5
Em modelos de dados em painel com efeito fixo, presume-se que as características individuais não observáveis que são constantes no tempo estão correlacionadas com as variáveis
explicativas.
Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
A média de X é igual a zero.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
O primeiro quartil da variável V é inferior a zero.
Julgue o seguinte item, relativo a processos estocásticos.
Em uma cadeia de Markov, a probabilidade de transição de um estado para outro é influenciada pela sequência completa de eventos anteriores
Supondo que os valores 3, 0, 0, 1, 4 constituam uma realização de uma amostra aleatória simples de tamanho n igual a 5 retirada de uma população com função de probabilidade
denota o parâmetro a ser estimado e x ∈ {0, 1, 2, … }, julgue o seguinte item.
A estimativa de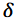 
pelo método dos momentos é igual a 1,6.
Acerca de econometria de dados em painel, julgue o seguinte item.
Em modelos de efeito aleatório, presume-se que as diferenças individuais não observadas não são correlacionadas com as variáveis explicativas ao longo do tempo, sendo tratadas como componentes aleatórios.
Considerando que representa uma variável aleatória com suporte ∈ {−2, −1, 0, +1, +2}, cuja função de distribuição de probabilidade é dada no quadro acima, na qual c é uma constante real positiva, julgue os próximos itens.
X segue uma distribuição contínua, pois c é uma constante real positiva.
Supondo que V e W sejam duas variáveis contínuas e mutuamente independentes, tais que P(V > 0) = 0,3 e P(W > 0) = 0,7, julgue o próximo item.
Considerando-se que as médias de V e W sejam iguais a 1 e que o coeficiente de variação de V seja igual ao dobro do coeficiente de variação de W , é correto concluir que a variância de V deve ser igual ao dobro da variância de W.
