Sobre os equipamentos da central de material e esterilização, o enfermeiro deve saber que
No trauma de tórax, as condições de imediato risco de morte que devem ser identificadas e tratadas na fase de avaliação inicial, são causadas, dentre outras, por
A Educação Continuada e a Educação Permanente em Saúde são as metodologias mais utilizadas para o desenvolvimento dos profissionais de enfermagem. As descrições abaixo referem-se às características dessas duas metodologias. I.( ) Representa uma continuidade do modelo escolar ou acadêmico, centralizado na atualização de conhecimentos, geralmente com enfoque disciplinar, em ambiente didático e baseado em técnicas de transmissão, com fins de atualização. II.( ) Incorpora o ensino e o aprendizado à vida cotidiana das organizações e às práticas sociais e laborais, no contexto real em que ocorrem. III.( ) Coloca as pessoas como atores reflexivos da prática e construtores do conhecimento e de alternativas de ação, ao invés de receptores. IV.( ) Centrada em cada categoria profissional, praticamente desconsiderou a perspectiva das equipes e diversos grupos de trabalhadores. Considerando que a Educação Continuada em Saúde está representada pela letra G e a Educação Permanente em Saúde pela letra H, a sequência correta, de cima para baixo, é
Uma distribuição estatística unimodal, com uma curva de frequência platicúrtica e sendo a média inferior à mediana e a mediana inferior à moda, caracteriza uma distribuição assimétrica à
Seja X uma variável aleatória uniformemente distribuída no intervalo (m , n) em que m e n são desconhecidos. Utiliza-se o método dos momentos para encontrar os estimadores para m e n ( IMAGEM , respectivamente). De uma amostra aleatória da respectiva população de tamanho 8, obteve-se uma média amostral igual a 6 e o momento de segunda ordem igual a 37,6875. Com base nos resultados desta amostra, encontra-se que o resultado da divisão de IMAGEM por IMAGEM apresenta um valor igual a
A amostra aleatória { X1, X2, X3, ... , X9 } foi extraída de uma população normal de tamanho infinito com variância (σ2)
desconhecida.
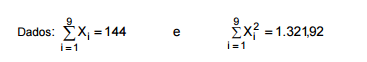
Com base nesta amostra, deseja-se obter um intervalo de confiança de 90% para a média μ da população utilizando a
distribuição t de Student levando em conta a tabela a seguir.
Este intervalo é igual a
Atenção: Para responder às questões de números 37 e 38 considere o modelo de regressão linear simples correspondente à equação Yi = α + βXi + ϵi (i = 1, 2, 3, ...) que é utilizado por uma empresa para prever o seu faturamento bruto (Y), em milhões de reais, em função do dispêndio com material promocional (X), também em milhões de reais. Os parâmetros α e β são desconhecidos, ϵi corresponde ao erro aleatório com as respectivas hipóteses do modelo de regressão linear simples e i refere-se à i-ésima observação das variáveis. As estimativas de α e β (a e b, respectivamente) foram obtidas pelo método dos mínimos quadrados, com base em 10 pares de observações (Xi , Yi ).
Considerando a equação da reta obtida pelo método dos mínimos quadrados, obtém-se que o acréscimo do faturamento bruto, em milhões de reais, cada vez que se decide aumentar em 1 milhão de reais o dispêndio com material promocional é de
A comissão de erradicação do trabalho infantil de um determinado Tribunal Regional do Trabalho analisa, por meio de seu canal
de denúncias, casos de desrespeito à legislação que regula o trabalho de menores de 18 anos. Suponha que a variável X, que
representa o número de denúncias mensais que são recebidas, tem distribuição de Poisson com média 9. Nessas condições, a
probabilidade de serem recebidas 2 ou 3 denúncias em um período de 10 dias é igual a
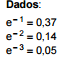
Atenção: Para responder às questões de números 49 a 53 utilize, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então: P(Z < 0,5) = 0,591; P(Z < 1) = 0,841; P(Z < 1,15) = 0,8951; P(Z < 1,17) = 0,879; P(Z < 1,2) = 0,885; P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2) = 0,977; P(Z < 2,06) = 0,98; P(Z < 2,4) = 0,997.
-------------------
Instrução: O enunciado a seguir refere-se às questões de números 49 a 51. Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
O valor de K, em anos, tal que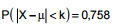 
é igual a
Atenção: Para responder às questões de números 49 a 53 utilize, dentre as informações dadas a seguir, as que julgar apropriadas.
Se Z tem distribuição normal padrão, então: P(Z < 0,5) = 0,591; P(Z < 1) = 0,841; P(Z < 1,15) = 0,8951; P(Z < 1,17) = 0,879; P(Z < 1,2) = 0,885; P(Z < 1,4) = 0,919; P(Z < 1,64) = 0,95; P(Z < 2) = 0,977; P(Z < 2,06) = 0,98; P(Z < 2,4) = 0,997.
-------------------
Instrução: O enunciado a seguir refere-se às questões de números 49 a 51. Considere que X é a variável aleatória, que representa as idades, em anos, dos trabalhadores de certa indústria. Suponha que X têm distribuição normal com média de μ anos e desvio padrão de 5 anos.
Uma amostra aleatória, com reposição, de 16 trabalhadores será selecionada e sejam X1, X2, ...X16 as idades observadas e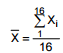 
a média desta amostra. Sabendo-se que a probabilidade de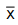 
ser superior a 30 anos é igual a 0,919, o valor de μ,
em anos, é igual a
Seja X uma variável aleatória com função densidade de probabilidade dada por:
onde k é uma constate real que torna f(x) uma função densidade de probabilidade.
Nessas condições, a função densidade de probabilidade da variável aleatória Y = 3X + 4, no intervalo 4 < y < 10 é dada por
Sobre a atuação do Ministério Público do Trabalho é correto afirmar que
Pessoas com transtorno de personalidade histriônica tendem a ser
Walter Trinca propôs o procedimento de Desenhos-Estórias (D-E) e de Família com Estórias (DF-E), como forma compreensiva de investigação psicológica. No D-E tradicional não é necessário o oferecimento de um tema, porém no DF-E pretende-se obter
Donald Winnicott descreveu uma conduta emocional da mãe a respeito de seu filho e apontou que os diferentes graus de perturbação psíquica se instalam a partir dos êxitos ou fracassos da sustentação, também denominada
