Considere os seguintes argumentos:
Argumento I
P1: Todos os inscritos no COREN são profissionais de Enfermagem.
P2: Todos os profissionais de Enfermagem são diplomados.
C: Todos os inscritos no COREN são diplomados.
Argumento II
P1: Todos os inscritos no COREN são profissionais de Enfermagem.
P2: Nenhum profissional de Enfermagem é bem remunerado.
C: Nenhum inscrito no COREN é bem remunerado.
Argumento III
P1: Todos os profissionais de Enfermagem são diplomados.
P2: Débora é diplomada.
C: Débora é uma profissional de Enfermagem.
Argumento IV
P1: Todos os profissionais de Enfermagem são diplomados.
P2: Débora não é profissional de Enfermagem.
C: Débora não é diplomada.
Assinale a afirmativa correta
A negação lógica da afirmação: "todos os boa-vistenses nasceram em Boa Vista e são roraimenses" é:
Em uma sequência, cada termo, a partir do terceiro, é a soma dos dois termos anteriores mais próximos. Se o sexto termo da sequência é 63 e o quarto é 24, qual o primeiro termo?
P: Todos os funcionários do sindicato usam crachá.
Q: Nenhum médico é funcionário do sindicato.
R: Alguns médicos gostam de futebol.
S: Todas as pessoas que usam crachá gostam de futebol.
Com base nas proposições acima, julgue o item.
Todos os funcionários do sindicato gostam de futebol
Em um aquário, há 4 peixes grandes e 6 pequenos. Para alimentá‐los, o criador gasta 400 g de ração por dia. Entre os peixes pequenos, exatamente 2 são vermelhos e os demais são azuis.Com base nesse caso hipotético, julgue o item.
Se dois peixes pequenos e um peixe grande morrem em certo dia, o criador deverá reduzir a ração diária para 2/3 da quantidade anterior.
P: Fátima não joga futebol e Luiz ouve música.
Q: Luiz corre ou Fátima dorme.
R: P ‐> Q.
A partir das proposições acima, julgue o item.
A negação da sentença P é a sentença: “Fátima joga
futebol e Luiz não ouve música”.
Um funcionário fez horas extras nos meses de agosto e de setembro, totalizando 16 horas extras. Sabendo que o número de horas extras feitas no mês de setembro superou o número de horas extras feitas no mês de agosto em 4 horas, então, o número de horas extras feitas no mês de setembro foi
Considere a sequência:
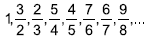
O produto entre o 8º, 17º e 27º termos é um número que
Um grupo de 3 amigos participa de um jogo de cartas, de modo que cada um possui 10 cartas idênticas à exceção de estarem numeradas de 1 a 10 em apenas um dos lados. Cada rodada do jogo consiste em cada participante escolher uma carta ao acaso (considerando a escolha da carta equiprovável entre as 10 cartas à disposição) e apresentar aos demais participantes. O jogo termina quando todas as cartas apresentadas na mesma rodada tiverem um valor par. Qual é a probabilidade de o jogo terminar na terceira rodada?
A: Gilberto namora Ana ou Daniel não compra um celular.
B: Se Gilberto não namora Ana, então Cássio está feliz.
C: Se Daniel não compra um celular, então Cássio não está feliz.
Sabendo que as sentenças acima são verdadeiras, julgue o item
Se Daniel não compra um celular, então Gilberto não
namora Ana.
Um anagrama é uma permutação das letras de uma palavra. Por exemplo, ERVIV é um anagrama da palavra VIVER. Com relação aos anagramas dessa palavra, julgue o item.
Existem mais de 20 anagramas da palavra VIVER em que as vogais estão juntas.
12 times de futebol, entre eles o Getabi e o Fadonense, se inscreveram em um torneio. Foram sorteados 4 times para compor o grupo A e mais 4 times para compor o grupo B. Os times restantes ficaram no grupo C. O primeiro jogo da competição será entre 2 times sorteados do grupo A.
Com base nesse caso hipotético, julgue o item
A probabilidade de o time Getabi estar no grupo B é maior que 40%.
Cinco amigos, Maria, Vitor, Marcos, Paulo e Lucas decidiram ir juntos a um restaurante para lmoçar. Antes de chegarem ao restaurante, combinaram o seguinte:
Se Maria comer arroz, então Vitor comerá feijão;
Se Marcos beber suco, então Lucas beberá refrigerante;
Se Paulo não beber refrigerante, então Vitor comerá lasanha;
Se Lucas não comer feijão, então Paulo comerá batatas.
Quando chegaram ao restaurante já não havia feijão e nem refrigerante. Assim, de acordo com o combinado entre os 5 amigos, pode-se afirmar que:
Uma loja de brinquedos para crianças possui bolinhas de 4 cores: 24 verdes, 36 azuis, 42 amarelas e 54 vermelhas. O dono da loja precisa guardar essas bolinhas em pacotes com a mesma quantidade e em cada pacote deve ter apenas bolinhas de uma mesma cor. Qual a quantidade mínima de pacotes que ele precisa para guardar todas essas bolinhas?
Observe a sequência regressiva abaixo:
62, 30, 14, X, 2, 0
Identifique o padrão estabelecido e marque a opção que indica o valor de X:

