Em uma tira de papel está escrito o número 7632591953. Dois cortes verticais são feitos na tira de forma a se obter 3 números. A menor soma possível dos 3 números obtidos é:
Uma estante contém 30 livros, que têm capa comum ou capa dura. Destes, 8 são livros de capa comum e são escritos em português. Apenas 20% dos livros são de capa dura e 1/3 destes são escritos em inglês. O número de livros escritos em português é, no máximo,
Foi modelado que o espalhamento de uma notícia em uma população — entendido como o percentual de indivíduos dessa população que recebe essa notícia por unidade de tempo — é diretamente proporcional ao percentual de indivíduos da população que já conhecem a notícia multiplicado pelo percentual de indivíduos dessa população que ainda não a conhecem até aquele instante. A constante k de proporcionalidade depende, entre outros fatores, do impacto da notícia na vida dos envolvidos e de propriedades dos meios de comunicação disponíveis.
Tendo como base essas informações e considerando que, para certa notícia, k = 1, julgue o item a seguir.
Se, em determinado instante, o espalhamento de uma notícia é igual a 16% por unidade de tempo, então, nesse instante, mais de 75% da população ainda desconhece a notícia.
Um hospital possui duas alas de UTI, totalizando 210 leitos. A primeira destina 25% dos leitos a pacientes infectados pela COVID-19; e a segunda, 50% dos leitos a pacientes com essa doença. Sabe-se que o número total de leitos destinados a pacientes com COVID-19, nas
duas UTIs, representa 40% do total de leitos de UTI no hospital. Desse modo, o número de leitos destinados a esses pacientes, na UTI com menor capacidade, é:
A tabela a seguir fornece, por sexo e por cargo pretendido, a quantidade total de candidatos inscritos em um concurso público.
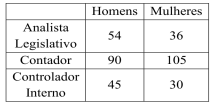
Escolhendo-se ao acaso um dos candidatos inscritos nesse concurso, a probabilidade de a pessoa escolhida ser mulher ou pretender um cargo de contador é de:
Sabendo que o sistema solar é composto por 8 planetas (Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano e Netuno), julgue o item.
Suponha-se que uma urna contenha 8 bolinhas e que, em cada uma, esteja escrito o nome de um planeta do sistema solar. Nesse caso, extraindo-se duas bolinhas sucessivamente ao acaso e com reposição, a probabilidade de que em nenhuma delas esteja escrito “Terra” é igual a 75%.
Uma primeira urna possui uma bola branca e duas pretas. Uma segunda urna possui duas bolas brancas e uma preta. Uma terceira urna, por sua vez, possui uma bola branca e uma preta. Uma pessoa vendada retira uma bola da primeira urna e a coloca na segunda. Em seguida, retira uma bola da segunda urna e a coloca na terceira. Por fim, retira uma bola da terceira urna.
Sabendo que todas a bolas são idênticas em forma e peso, quantas possibilidades há de que a bola retirada da terceira urna seja preta?
Sabendo que o sistema solar é composto por 8 planetas (Mercúrio, Vênus, Terra, Marte, Júpiter, Saturno, Urano e Netuno), julgue o item.
Escolhendo-se um dos planetas do sistema solar ao acaso, a probabilidade de o planeta começar e terminar com uma consoante é inferior a 25%.
Sabe‐se que, a cada 10 pênaltis marcados a favor de um time de futebol, 6 são cobrados por Bárbara e 4 por Débora. A probabilidade de um pênalti ser convertido por Bárbara é de 90% e a de ser convertido por Débora, de 80%.
Com base nessa situação hipotética, julgue o item.
A probabilidade de um pênalti ser cobrado e convertido por Bárbara é de 54%.
Sabe‐se que, a cada 10 pênaltis marcados a favor de um time de futebol, 6 são cobrados por Bárbara e 4 por Débora. A probabilidade de um pênalti ser convertido por Bárbara é de 90% e a de ser convertido por Débora, de 80%.
Com base nessa situação hipotética, julgue o item.
Se um pênalti foi convertido, então a probabilidade de ele ter sido cobrado por Bárbara é superior a 60%.
Os professores João, Carlos e Luis ministrarão um curso de primeiros socorros em que serão ensinados os seguintes procedimentos.
I fazer massagem cardíaca
II desengasgar
III estancar sangramentos
IV amenizar queimaduras
V desafogar
VI cuidar de fraturas
Cada professor ensinará exatamente dois procedimentos, e o mesmo professor que ensinar o procedimento desafogar ensinará também o procedimento desengasgar.
Considerando essa situação hipotética, julgue o próximo item.
Selecionando-se ao acaso o professor que ensinará o procedimento fazer massagem cardíaca, a probabilidade de Luis ser o escolhido é maior do que 40%.
Texto 1A6-I
Cinco pessoas (Arnaldo, Bernardo, Cláudio, Diógenes e Ernesto), suspeitas de determinada contravenção, são chamadas para acareação por uma autoridade policial. Exatamente dois deles são culpados, e as seguintes declarações foram feitas durante o depoimento:
I. Arnaldo disse que os culpados não foram Ernesto nem Bernardo;
II. Bernardo disse que os culpados não foram Arnaldo nem Cláudio;
III. Cláudio disse que os culpados não foram Bernardo nem Diógenes.
No texto 1A6-I, se 3 pessoas forem aleatoriamente escolhidas entre os 5 suspeitos, então a probabilidade de os dois culpados serem escolhidos será igual a
Considere os seguintes conjuntos:

e, assim, sucessivamente.
Com base nessas informações, julgue o item que se segue:
Escolhendo-se aleatoriamente um integrante do conjunto P, a probabilidade de ele ter entre dois e três anos de experiência no exercício do cargo é dada por n(P2 — P3)/n(P3), em que n(X) indica o número de elementos do conjunto X e P2 — P3 é o conjunto formado pelos indivíduos que estão em P2, mas não estão em P3
Sabe‐se que, a cada 10 pênaltis marcados a favor de um time de futebol, 6 são cobrados por Bárbara e 4 por Débora. A probabilidade de um pênalti ser convertido por Bárbara é de 90% e a de ser convertido por Débora, de 80%.
Com base nessa situação hipotética, julgue o item.
A probabilidade de esse time desperdiçar um pênalti é maior que 15%.
Considerando dois eventos aleatórios A e B, tais que P(A|B) = 1/3, P(B|A) = 0,5 e P(A B) = 0,8, julgue os seguinte item.
P(A) > P(B).

