Temos uma sequência de quatro números inteiros positivos, (a1, a2, a3, a4), em que cada número é obtido somando 3 unidades ao número que antecede na sequência. Sabendo que a soma dos números da sequência é igual a 106, podemos afirmar corretamente que o valor de a1 é igual a:
Em uma empresa petroquímica com 50 funcionários, foi realizada uma pesquisa sobre a confiança nos equipamentos de proteção individual (EPIs) disponibilizados pela empresa. Todos os 50 funcionários responderam entre as opções confiam ou não confiam. Com isso, foi constatado que o número de funcionários que confiam nos EPIs é igual a dos que não confiam e que o número de homens que confiam nos EPIs é igual a 9. Além disso, o número de homens que trabalham na empresa é igual a do número de mulheres que trabalham na empresa.
Com base nesse caso hipotético, é correto afirmar que, na empresa, o número de funcionários que não confiam nos EPIs e que são mulheres é igual a
Uma loja vende pequenas árvores de Natal cônicas. Esses itens são guardados em caixas, que são paralelepípedos de 50 cm de altura e base quadrangular de 20 cm de aresta.
Com base nesse caso hipotético, julgue o item
Admitindo-se que a proporção entre a árvore de Natal e a caixa em formato de paralelepípedo deva ser mantida, para uma árvore com dimensões 40% maiores, a caixa necessária terá exatamente 54,88 dm3 de volume.
Com relação a tópicos de matemática, julgue o item que se segue.
O coeficiente do termo independente no desenvolvimento de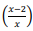 
10 é -4032.
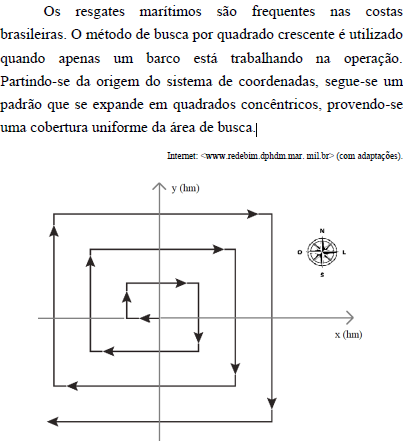
O gráfico anterior ilustra, em um sistema de coordenadas cartesianas ortogonais xOy, parte da trajetória percorrida por determinado barco que realizou o método de busca por quadrado crescente descrito no texto precedente. Os dois primeiros movimentos desse barco — primeiro para o oeste e depois para o norte — têm comprimentos iguais a 1 hectômetro (hm); os dois próximos movimentos têm comprimentos iguais a 2 hm; os dois movimentos seguintes a estes têm comprimentos iguais a 3 hm; e assim sucessivamente.
Considerando as informações apresentadas, julgue o item subsequentes, a partir dessa situação hipotética
Logo após ter percorrido, pela segunda vez, um segmento de reta de comprimento igual a 7 hm, o barco navegou uma distância total maior do que 60 hm.
Os professores João, Carlos e Luis ministrarão um curso de primeiros socorros em que serão ensinados os seguintes procedimentos.
I fazer massagem cardíaca
II desengasgar
III estancar sangramentos
IV amenizar queimaduras
V desafogar
VI cuidar de fraturas
Cada professor ensinará exatamente dois procedimentos, e o mesmo professor que ensinar o procedimento desafogar ensinará também o procedimento desengasgar.
Considerando essa situação hipotética, julgue o próximo item.
Se Carlos ensinar o procedimento cuidar de fraturas, então, selecionando-se ao acaso os professores que ensinarão os outros procedimentos, a chance de que João ensine o procedimento desafogar é maior do que 45%.
Com relação a polígonos regulares e convexos, julgue o item a seguir.
A área de um hexágono regular inscrito em uma circunferência de raio √2 cm é igual a 3√3 cm2.
Durante um atendimento, o cliente de um banco relata ao gerente de atendimento sua disponibilidade para investir R$400.000,00. O gerente tem ao seu dispor 5 opções de investimento: renda fixa, CDB, fundo de ações, LCI e LCA. Ao cliente foi oferecida uma carteira diversificada de
20%, 10%, 30%, 15% e 25%, respectivamente.
Sendo assim, verifica-se que o valor sugerido para
A sequência de Fibonacci é bastante utilizada para exemplificar sequências definidas por recorrência, ou seja, sequências em que se pode determinar um termo a partir do conhecimento de termos anteriores. No caso da sequência de Fibonacci, escreve-se que Tn+2 = Tn+1 + Tn e, desse modo, pode-se obter um termo qualquer conhecendo-se os dois termos anteriores.
Considerando o exposto acima, determine o termo T2021 da sequência de Fibonacci, sabendo que T2018 = m e T2020 = p.
Para os seis primeiros meses de um investimento, a evolução, em milhares de reais, de um certo investimento de R$ 3.000,00 é expressa pela fórmula, onde M(x) = , onde M(x) indica quantos milhares de reais a pessoa poderá retirar após x meses desse investimento. Um cliente pretende deixar esse investimento por seis meses.
Nesse caso, de quanto será a sua perda, em reais, em relação ao máximo que ele poderia ter retirado?
Um banco tem agências em três regiões do país. Em cada região, trabalha-se com a comercialização de três segmentos: seguros (X), previdência (Y) e consórcios (Z). Cada equação linear que compõe o sistema abaixo representa a capacidade de uma regional produzir valor agregado para o banco, em cada segmento de atuação (lado esquerdo das equações), visando ao alcance das metas de lucro operacional em milhares de reais (lado direito das equações).
De acordo com esses dados, verifica-se que a contribuição de um dado segmento que atinge exatamente a meta de sua região é de
Ainda com base nos dados apresentados na tabela 4A3-I, assinale a opção que representa a previsão de consumo, em unidades, de resmas de papel para o mês de junho de 2021 naquele órgão público, calculada por meio do método do último período.
• A é o conjunto-solução da equação x2 –9x +18 = 0.
• B é o conjunto dos números inteiros da solução da inequação |x –12| < 2.
• C é o conjunto dos números naturais pares.
• Sendo D um conjunto que contém A, o complementar relativo de A em relação a D é igual a {0, 2, 5, 7, 9}.
• Sendo E um conjunto que contém B, o complementar relativo de B em relação a E é igual a {5, 6, 7, 20}.
Considerando as premissas acima apresentadas, é correto afirmar que (D ∪ E) ∩ C é igual ao seguinte conjunto:
Sejam p e q dois números tais que p + q = 17 e p2 + q2 = 169, com p > q, julgue o item.
Se A = (p, q, p − 2q) e B = (48, x, y) são grandezas inversamente proporcionais, então x − y = 8.
Uma função f ݂: R → R, do 2.° grau, é tal que f(3) = 0, f(8) – f(6) = 11 e f(10) = 35. Considerando essas informações, julgue o item.
f(100) ≤ 5.000.
