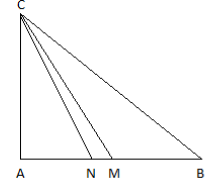
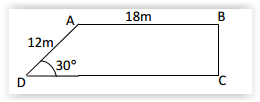
Considere o triângulo retângulo ABC com os catetos AB e AC medindo, respectivamente, 40 e 30. Se M é o ponto médio de AB e N é a intersecção da bissetriz do ângulo ACB com o lado AB, qual é a área do triângulo CNM?
A forma trigonométrica do número complexo z = -√3 + 3i é representada por:
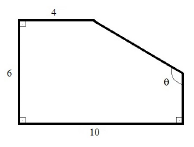
O pentágono apresentado na figura acima possui área igual a
Sabendo‐se que o cos(30) é igual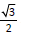 
a é correto concluir que o sen2(15) vale
O retângulo ABCD tem dimensões AB = 2 e BC = 4. Os pontos M e N são médios dos lados BC e CD, respectivamente.
O cosseno do ângulo AMN é igual a
No décimo dia do mês de agosto, a tábua das marés indicou que a maré alta e a maré baixa, na praia do Chapéu Virado, na ilha do Mosqueiro, atingiram 3,5 metros e 0,7 metros de altura, respectivamente. Sabe-se também que a baixa-mar ocorreu ao meio-dia e à meia-noite, enquanto que preamar ocorreu às 06h e às 18h. Considerando que a altura da maré em função do tempo h (t) é dada por um modelo matemático do tipo h(t) - a +b. sen(c.t + d), com a, b, c e d, constantes reais, o número de vezes que a maré atingiu à altura de 2,8 metros, entre 03h e 19h é igual a
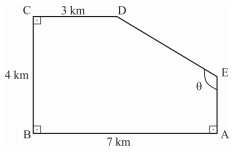
A figura seguinte ilustra um terreno pentagonal no qual será semeado um cultivar que, para desenvolver-se livre de parasitas, receberá a aplicação, para cada hectare, de 0,5 L de um herbicida especial cujo litro custa R$ 60.
Os cinco lados do terreno são retos e formam o pentágono ABCDE antecedente, em que os ângulos nos vértices A, B e C são retos, AB = 7 km, BC = 4 km e CD = 3 km. Sabe-se também que o ângulo no vértice E é θ, em que tg θ = –2 e tg (π – θ) = 2.
Na situação apresentada, o custo do herbicida a ser aplicado no terreno será de
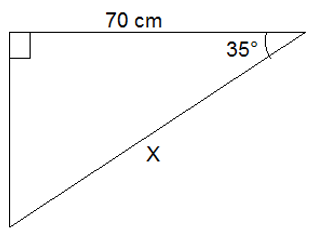
Qual é a área do triângulo a seguir?
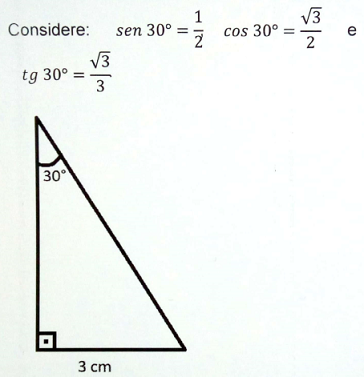
Qual o valor de x? Dado: sen35°=0,57; cos35°=0,82; tan35°=0,7
A rampa de acesso de um estacionamento forma um ângulo de 12° com o solo (horizontal). Sabendo-se que a altura em relação ao solo no final da rampa será de 80 (oitenta) centímetros, qual será o comprimento total, em metros, desta rampa? (Dados: sen 10° = 0,20; cós 10° = 0,98; tg 10° = 0,21).
O esquema mostra o percurso de um barco ao longo de todo o seu trajeto.
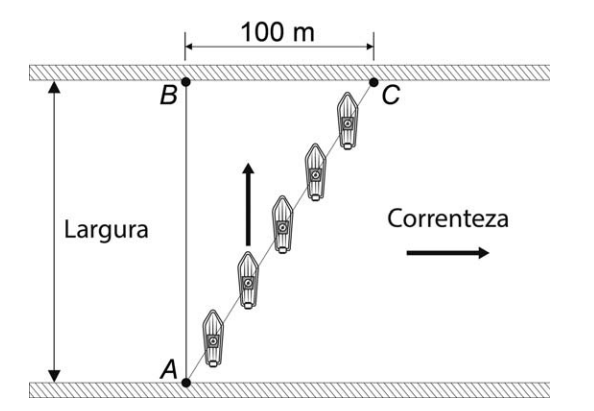
O barco mantém-se sempre na mesma direção, perpendicular à correnteza.
Porém, devido à ação desta, sua trajetória é direcionada para o ponto C, no outro lado da margem, a 100 metros do ponto inicial de destino B. Sabe-se também que o ângulo formado entre o novo trajeto e a direção perpendicular à margem, no ponto A, é de 30°.
A distância, em metro, percorrida pelo barco é de
O menor valor que a função f(x) = sec2x - tg2x - cos x pode assumir é
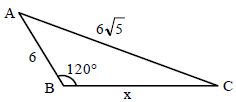
Pelo triângulo ABC, o valor de x2 + 6x é
Seja a expressão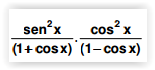 
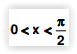
definida em 
. Ao simplificá-la, obteremos:
Fábio precisa comprar arame para cercar um terreno no formato a seguir, retângulo em B e C. Considerando que ele dará duas voltas com o arame no terreno e que não terá perdas, quantos metros ele irá gastar? (considere √3 =1,7; sen30º=0,5; cos30º=0,85; tg30º=0,57).
