Certa escola tem 15 classes no período matutino e rascunho 10 classes no período vespertino. O número médio de alunos por classe no período matutino é 20, e, no período vespertino, é 25. Considerando os dois períodos citados, a média aritmética do número de alunos por classe é
Em uma instituição de ensino, a nota final de cada aluno RAS C U NHO é calculada pela média aritmética ponderada das notas dos quatro bimestres, com pesos 1, 2, 3 e 4, para os bimestres de 1 a 4, respectivamente. Para ser aprovado, o aluno tem que atingir nota final 5. Sendo assim, um aluno que tirou no primeiro, segundo e terceiro bimestres notas 4, 6 e 3, respectivamente, precisa tirar, no quarto bimestre para ser aprovado, no mínimo, uma nota igual a
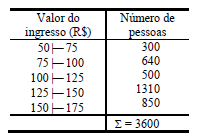
A tabela seguinte informa a quantidade de pessoas que compraram ingressos antecipados de um determinado show, cujos
preços eram modificados semanalmente. O percentual de pessoas que adquiriram o ingresso por menos de R$ 125,00 foi
O gráfico apresenta informações do lucro, em reais, so- R ascunho
bre a venda de uma quantidade, em centenas, de um
produto em um hipermercado.
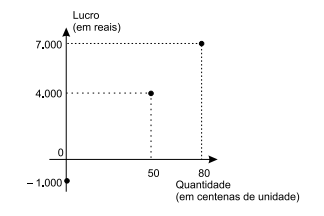
Sabendo-se que é constante a razão entre a variação do
lucro e a variação da quantidade vendida e que se pretende
ter um lucro total não menor que R$ 90.500,00 em
10 dias de venda desse produto, então a média diária
de unidades que deverão ser vendidas, nesse período,
deverá ser, no mínimo, de
A medida estatística que separa as metades superior e inferior dos dados amostrados de uma população é chamada de:
A variância amostral é uma medida de dispersão que mostra
o quão dispersos são os dados da amostra em relação à sua
média. Com base nessa informação, a variância amostral
para a amostra 3, 6, 8, 7, 6 e 12 é igual a
Considerando que, em um estudo nacional sobre o sistema penitenciário brasileiro para avaliar a qualidade das instalações bem como para identificar os casos de superlotação, a unidade observacional tenha sido a cela onde se encontravam os detentos, julgue os itens que se seguem.
Caso outra amostra de presídios fosse selecionada aleatoriamente, a estimativa pontual do parâmetro estudado poderia ser diferente da estimativa encontrada na amostra apresentada.
Uma amostra de vinte presídios foi selecionada para que fosse verificada a quantidade média de indivíduos por cela. A amostra foi estratificada por localização: capital (C) e interior (I). A quantidade média de indivíduos por cela nas capitais é igual a 10, ao passo que a quantidade média de indivíduos por cela nas cidades do interior é igual a 15. Considerando essa situação hipotética, julgue os itens a seguir.
Se a alocação da amostra nos estratos ocorrer de forma uniforme, o número médio estimado de presos por cela para toda a população será maior que 14.
Considerando que, em um estudo nacional sobre o sistema penitenciário brasileiro para avaliar a qualidade das instalações bem como para identificar os casos de superlotação, a unidade observacional tenha sido a cela onde se encontravam os detentos, julgue os itens que se seguem.
Nesse estudo, uma amostragem aleatória simples sairá mais cara que uma amostragem por conglomerados.
As variáveis Y e X são relacionadas deterministicamente segundo a expressão matemática Y = 0.6 X. Uma pessoa escolhe vinte valores diferentes para X e calcula os Y correspondentes pela expressão Y = 0.6X.
O coeficiente de correlação entre os valores de X e os correspondentes valores de Y é igual a
Um analista observou que a média das remunerações recebidas pelos 100 empregados que responderam a uma determinada pesquisa estava muito baixa: R$ 2.380,00. Após investigar, verificou que 15% das respostas estavam com valor nulo e todas elas eram referentes às respostas dos empregados que se recusaram a responder a esse quesito, embora recebessem remuneração.
Inicialmente, o analista registrou variância dos salários, em reais2 , igual a 2.835.600,00.
Retirando as observações nulas, a média dos quadrados dos salários dos respondentes é, em reais2 , aproximadamente,
Estabelece-se um modelo AR(1) aos seguintes dados: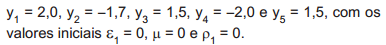 
O valor inteiro mais próximo de 
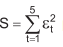para os dados apresentados é
Uma amostra aleatória simples de tamanho n é tomada de uma população de tamanho N. Sabe-se que N = 10 n e que a variância populacional é σ2. A variância da média amostral é dada por
