Observe o modelo de regressão linear simples, em que β0 e β1 são parâmetros do modelo e ε é o erro aleatório:
y = β0+ β1 x1+ ε
Nesse caso, o parâmetro β1 corresponde:
Entende-se por pesquisa científica a atividade que busca responder a problemas ou conhecer e entender fenômenos que ocorrem em diversas áreas do saber. Para tanto, devem ser utilizados métodos científicos. Quanto à abordagem, a metodologia científica pode ser qualitativa ou quantitativa.
Uma escala que permite avaliar variáveis qualitativas com processos estatísticos é a escala de:
Certo indivíduo afirmou que a distribuição exponencial
é adequada como premissa atuarial para se modelar o
tempo de vida de um recém-nascido.
Tendo em vista a assertiva acima, pode-se dizer que está
Uma equipe de trabalho reúne 4 auditores e 6 analistas. Se três pessoas dessa equipe forem selecionadas aleatoriamente para formar um pequeno grupo de trabalho, a probabilidade de que esse grupo seja formado por dois analistas e um auditor é igual a
Considere a amostra de idades a seguir:
25, 18, 21, 21, 22, 22, 23, 23, 25, 26, 28, 29, 31, 30, 52, 28, 55, 18, 22, 20, 27.
Em relação a essa amostra, avalie as afirmativas a seguir.
I. A mediana é igual a 25.
II. A média é maior do que a mediana.
III. A moda é menor do que a mediana.
Está correto o que se afirma em
Uma reta de regressão linear simples foi obtida a partir do modelo
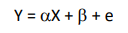
pelo método de mínimos quadrados usual e mostrou as seguintes estimativas dos coeficientes: a = 3,4 e b = 0,5; além disso, obteve-se um coeficiente de correlação amostral igual a 0,9.
Com base nesses dados, avalie se as afirmativas a seguir estão corretas.
I. A porcentagem da variação total dos dados que é explicada pela regressão é menor do que 60%.
II. A reta de regressão obtida ajusta bem o modelo.
III. O intercepto a = 3,4 mostra que a valor grandes de x correspondem valores grandes de y.
Está correto o que se afirma em
O menor tamanho da amostra aleatória simples para que possamos garantir, com 99% de confiança, que a proporção de sucessos amostral não diferirá da proporção de sucessos populacional por mais de 1% deve ser aproximadamente igual a
[dado: se Z ~N(0, 1), P[ Z < 2,58] = 0,995]
A mediana é a realização que ocupa a posição central da série de observações, quando estão ordenadas em ordem crescente. Assim, se as cinco observações de uma variável forem 3, 4, 7, 8 e 8, a mediana é o valor 7,
correspondendo à terceira observação.
O pioneiro da aplicação da estatística ao controle da qualidade foi Walter A. Shewhart, dos Laboratórios Bell,
que em 1924 preparou o primeiro rascunho do viria a ser conhecido como carta de controle.
Em certa pesquisa de opinião, o valor X = -1 foi atribuído para cada entrevistado que se declarou insatisfeito com determinado serviço, enquanto que o valor X = 1 foi atribuído para cada entrevistado que se declarou satisfeito com esse mesmo serviço.
Considerando-se a situação hipotética apresentada, é correto afirmar que, caso a média amostral dessa variável X seja igual a 0,5, então a mediana amostral de X será igual a
Um pesquisador deseja extrair uma amostra aleatória estratificada de tamanho n = 10 de uma população de tamanho N = 1.000. Essa população consiste de três estratos de tamanhos N1 = 500, N2 = 300, e N3 = 200, e os desvios-padrão da variável de interesse correspondentes a esses estratos valem, respectivamente, σ1 = 1, σ2 = 5, e σ3 = 5.
Nessa situação hipotética, considerando-se que o custo da pesquisa seja constante, não dependendo, portanto, do estrato, conclui-se, com base no método da alocação ótima de Neyman, que o tamanho da amostra referente ao estrato 2 deve ser igual a
Suponha que existam três eventos A, B e C que podem estar associados à ocorrência de uma doença D, com as seguintes probabilidades condicionais.
P(D|A) = 0,5
P(D|B) = 0,2
P(D|C) = 0,1
Nessa situação hipotética, sabendo que os eventos A, B e C formam uma partição do espaço amostral e que as probabilidades de ocorrência desses eventos são, respectivamente, P(A) = 0,1, P(B) = 0,1 e P(C) = 0,8, o valor da probabilidade P(C|D) é igual a
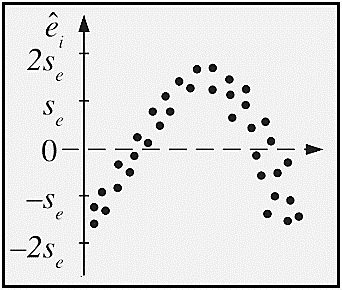
Para verificar se um modelo de regressão linear é adequado, precisa investigar se as suposições feitas para o desenvolvimento do modelo estão satisfeitas, assim é importante verificar o comportamento do modelo usando o conjunto de dados observados, prestando atenção as discrepâncias entre os valores observados e os valores ajustados pelo modelo, ou seja, fazendo uma análise dos resíduos.
Analise o gráfico abaixo sobre resíduos e assinale a alternativa correta.
Ao lançar um dado de 6 faces com números de 1 a 6 ao chão, a probabilidade de o número da face voltada para cima ser par ou maior que 3 é aproximadamente igual a:


