Sejam os arcos de 480° e −4π/3 rad. No ciclo trigonométrico, esses arcos são tais que ambos estão no
Considere a matriz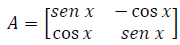 
e as seguintes proposições:
I- Se Paris está na França então o determinante de A é igual a 0 (zero).
II- Se Paris está na Inglaterra então o determinante de A é igual a 1 (um).
III- Se Paris está na França, então o determinante de A é igual a 1 (um).
IV- Se Paris está na Inglaterra, então o determinante de A é igual a 0 (zero).
Então, entre as quatro proposições acima, o rol completo da(s) proposição(ões) correta(s) é:
Se x é um arco do 2º quadrante, o conjunto solução da inequação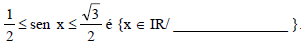 
Sejam as funções trigonométricas f(x) = 2 sen 2x e g(x) = sen x cujos gráficos são construídos no mesmo plano cartesiano. Marque a alternativa que corresponde ao número de vezes em que os gráficos das funções f e g se interceptam no intervalo [0,2π[.
As coordenadas usualmente utilizadas na localização de um ponto sobre a superfície terrestre são a latitude e a longitude. Para tal, considera-se que a Terra tem a forma de uma esfera.
Um meridiano é uma circunferência sobre a superfície da Terra que passa pelos polos Norte e Sul, representados na figura por PN e PS. O comprimento da semicircunferência que une os pontos PN e PS tem comprimento igual a 20 016 km. A linha do Equador também é uma circunferência sobre a superfície da Terra, com raio igual ao da Terra, sendo que o plano que a contém é perpendicular ao que contém qualquer meridiano.
Seja P um ponto na superfície da Terra, C o centro da Terra e o segmento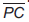 
um raio, conforme mostra a figura. Seja ϕ o ângulo que o segmento 
faz com o plano que contém a linha do Equador. A medida em graus de ϕ é a medida da latitude de P.
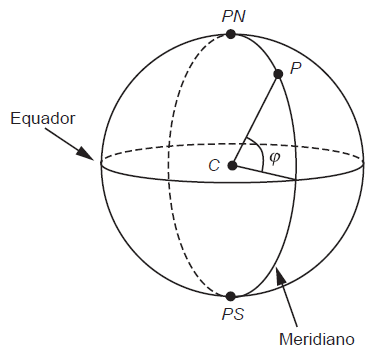
Suponha que a partir da linha do Equador um navio viaja subindo em direção ao Polo Norte, percorrendo um meridiano, até um ponto P com 30 graus de latitude.
Quantos quilômetros são percorridos pelo navio?
Um grupo de engenheiros está projetando um motor cujo esquema de deslocamento vertical do pistão dentro da câmara de combustão está representado na figura.
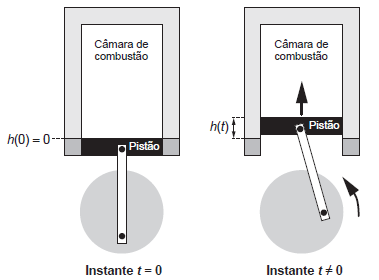
A função h(t) = 4 + 4sen 
definida para t ≥ 0 descreve como varia a altura h, medida em centímetro, da parte superior do pistão dentro da câmara de combustão, em função do tempo t, medido em segundo. Nas figuras estão indicadas as alturas do pistão em dois instantes distintos.
O valor do parâmetro β, que é dado por um número inteiro positivo, está relacionado com a velocidade de deslocamento do pistão. Para que o motor tenha uma boa potência, é necessário e suficiente que, em menos de 4 segundos após o início do funcionamento (instante t = 0), a altura da base do pistão alcance por três vezes o valor de 6 cm. Para os cálculos, utilize 3 como aproximação para π.
O menor valor inteiro a ser atribuído ao parâmetro β, de forma que o motor a ser construído tenha boa potência, é
Em um retângulo
Uma embarcação se encontra no ponto B, situado a 1 km da costa, de frente para o ponto L. O destino dessa embarcação é o farol, localizado no ponto F, distante √3 km do ponto L. Para efeito de orientação, o comandante dessa embarcação precisa calcular a medida do ângulo 
.
O ângulo 
mede, em grau,
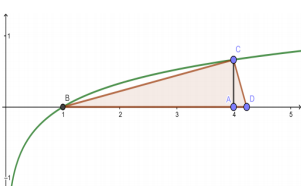
Seja um triângulo retângulo BCD, com ângulo reto em C e altura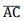 
relativa à hipotenusa BD. Seus vértices B e C são pontos do gráfico de f(x) = log8x cujas abscissas são, respectivamente, 1 e 4. Determine a área do triângulo BCD.
Ao subtrair cos 225° de sen 420°, obtém-se
Considere x um arco do 3º quadrante e cotangente de x igual a ctg x. Se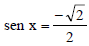 
, então o valor d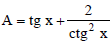e 
é
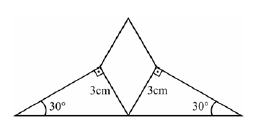
A figura representa o logotipo de uma empresa que é formado por 2 triângulos retângulos congruentes e por um losango. Considerando as medidas indicadas, a área do losango, em cm2, é
Rosângela gosta muito de viajar. Em sua última viagem, resolveu visitar a África, curiosa de conhecer as famosas pirâmides do Egito. Vendo a pirâmide de Quéfren, localizada no vale do Nilo, o guia turística a informou de que a inclinação das faces da pirâmide era de aproximadamente 53° com a horizontal. Por medidas de segurança eles ficaram a uma distância de 84 metros perpendicularmente à base, de onde se tem um ângulo de elevação ao topo da pirâmide de 37°. Quanto vale, em metros, a extensão da aresta da base ao ápice da pirâmide? Use sen 37º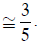 
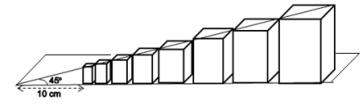
Um professor de matemática tirou o final de semana para organizar sua estante de livros e em uma das prateleiras ele usou a seguinte formação: foram dispostos oito livros, um ao lado do outro, de acordo com suas respectivas espessuras e alturas, de modo que um sempre tivesse o dobro da espessura do outro e o da frente seja sempre maior que o de trás, formando com a base da prateleira onde estavam, um triangulo retângulo com um ângulo de 45º, como expresso na figura abaixo. Qual a altura, em metros, do maior livro, sabendo que o menor livro mede 0,2cm de espessura?
Dados: use √3 = 1,7.
Considere a seguinte figura
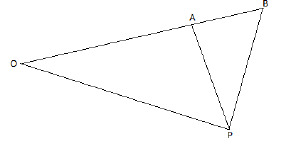
Onde os ângulos OPA e POA medem 30 o, o ângulo APB mede 45o e o segmento OP mede (3 + √3)m. O segmento AB mede
