O dono de um restaurante situado às margens de uma rodovia percebeu que, ao colocar uma placa de propaganda de seu restaurante ao longo da rodovia, as vendas aumentaram. Pesquisou junto aos seus clientes e concluiu que a probabilidade de um motorista perceber uma placa de anúncio é 
Com isso, após autorização do órgão competente, decidiu instalar novas placas com anúncios de seu restaurante ao longo dessa rodovia, de maneira que a probabilidade de um motorista perceber pelo menos uma das placas instaladas fosse superior a 
.
A quantidade mínima de novas placas de propaganda a serem instaladas é
Em um determinado ano, os computadores da receita federal de um país identificaram como inconsistentes 20% das declarações de imposto de renda que lhe foram encaminhadas. Uma declaração é classificada como inconsistente quando apresenta algum tipo de erro ou conflito nas informações prestadas. Essas declarações
consideradas inconsistentes foram analisadas pelos auditores, que constataram que 25% delas eram fraudulentas.Constatou-se ainda que, dentre as declarações que não apresentaram inconsistências, 6,25% eram fraudulentas.
Qual é a probabilidade de, nesse ano, a declaração de um contribuinte ser considerada inconsistente, dado que ela era fraudulenta?
Treze carros de mesmo modelo serão aleatoriamente enfileirados, lado a lado. Quatro deles são azuis, três são pretos, cinco brancos e um vermelho. Cada carro tem uma numeração que também será registrada em um cartão, e estes, colocados em uma mesma urna. Ao se retirar aleatoriamente os cartões, um a um, identifica-se o carro e o estaciona. Qual a probabilidade de que todos os carros de mesma cor fiquem juntos?
João e Adilson estão em uma reunião com todos os outros supervisores da empresa em que trabalham. Eles estão sentados juntos a uma mesa retangular, cada um (João e Adilson) em uma ponta. Entre eles, de um lado, há três pessoas e, do outro, duas pessoas. Um garçom coloca, aleatoriamente, 7 pratos na mesa, um na frente de cada lugar. Em um desses pratos, está colado um envelope com a quantia de R$ 1.000,00. Qual é a probabilidade de João ou Adilson receberem o prato com o envelope?
A respeito do princípio da contagem, de permutações e de probabilidade, julgue o item. Escrevendo‐se cada letra da palavra AUXILIAR em uma bola e colocando as oito bolas em uma urna, a probabilidade de se retirar duas bolas e ambas serem consoantes é superior a 12%.
12 times de futebol, entre eles o Getabi e o Fadonense, se inscreveram em um torneio. Foram sorteados 4 times para compor o grupo A e mais 4 times para compor o grupo B. Os times restantes ficaram no grupo C. O primeiro jogo da competição será entre 2 times sorteados do grupo A.
Com base nesse caso hipotético, julgue o item
A probabilidade de o Getabi e o Fadonense fazerem o primeiro jogo do torneio é maior que 1%.
João vai viajar e precisa escolher 3 camisas para levar. Sabendo-se que ele dispõe de 5 camisas distintas para escolher, ao todo, de quantas formas distintas ele pode fazer essa escolha?
Em uma mostra de cinema, há 6 filmes para serem exibidos em 6 dias, cada filme em um dia diferente. Há 3 filmes de comédia e 3 de terror. Com base nessa situação hipotética, julgue o item.
Se um crítico escreveu resenhas para 3 filmes da mostra de cinema, então a probabilidade de ele ter escrito resenhas exatamente para os 3 filmes de comédia é menor que 4%.
José envia uma mesma mensagem para vários amigos. A probabilidade que José envie a mensagem para Augusto é 7/10. Ainda, em geral a probabilidade de as mensagens de José para Augusto serem filtradas para a caixa de spam (e, portanto, não serem entregues na caixa de entrada principal de Augusto) é 6/10.
Logo, a probabilidade de Augusto não receber a mensagem de José em sua caixa principal é:
Em um aquário, há 4 peixes grandes e 6 pequenos. Para alimentá‐los, o criador gasta 400 g de ração por dia. Entre os peixes pequenos, exatamente 2 são vermelhos e os demais são azuis.Com base nesse caso hipotético, julgue o item.
Escolhendo‐se ao acaso um peixe qualquer do aquário, a probabilidade de se ter escolhido um peixe pequeno azul é maior que 50%.
Uma construtora comprou um grande lote de peças de mármore diretamente de uma grande marmoraria para a construção de casas populares. As peças vêm embaladas de forma individual. Um funcionário da construtora inspeciona cinco peças para verificar o número de peças quebradas ou danificadas. A perda de materiais na construção civil é bastante elevada. Os percentuais de perdas de alguns materiais preocupam as empresas. Sabendo-se que um grande lote contém 1% de peças quebradas ou danificadas, analise as seguintes afirmativas:
- A probabilidade de o funcionário encontrar no máximo uma peça quebrada ou danificada é 1,04x(0,99)4 .
- A probabilidade de o inspetor encontrar pelo menos uma peça quebrada ou danificada é 1 − 0,995 .
- A probabilidade de o inspetor encontrar todas as peças defeituosas é (0,01)2
Seja P( X ) a probabilidade de ocorrência de um evento X. Dados 2 eventos A e B, a probabilidade de ocorrer pelo menos um dos dois eventos é igual a 4/5 e a probabilidade de ocorrer o evento A e o evento B é igual a 1/10. Se P( A ) é igual a 1/2, então P( B ) é igual a
Pesquisa realizada com um grupo de 100 pessoas jovens de uma cidade do interior do Estado de São Paulo mostrou que:
Com base nessa pesquisa, qual é a probabilidade de que ao se escolher, aleatoriamente, uma dessas pessoas, de que a pessoa escolhida seja um jovem graduado fumante ou um jovem não fumante?
Um candidato ao participar de um concurso de matemática depara-se com três questões com as seguintes pontuações q1=20 pontos, q2=30 pontos e q3=50 pontos. Se a probabilidade do candidato acertas as questões são de 0,3; 0,8 e 0,4 respectivamente, qual o valor esperado da pontuação deste candidato?
No Pisa, avaliação internacional da OCDE, o cenário é difícil para jovens de 15 a 16 anos. Desde 2009, o Brasil não apresenta avanços nesta avaliação. Com o gráfico abaixo vemos a evolução da média do Brasil em Matemática no Pisa. Temos um grande desafio - 46,5% de nossos alunos na rede pública estão abaixo do nível 1 em Matemática.
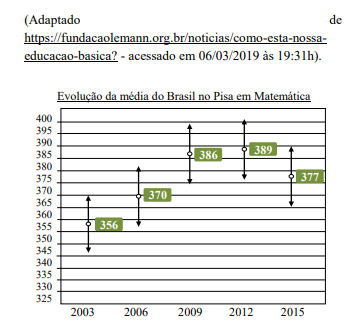
Seja xi a média em Matemática obtida pelo Brasil no Pisa e
