As técnicas de amostragem podem ser classificadas em:
De uma amostra aleatória simples de tamanho n = 400 retirada de uma população normal, obteve-se as seguintes estatísticas.

Deseja-se testar a hipótese H0: μ ≥ 20 contra a hipótese H1: μ < 20 com nível de significância de 5%, na qual μ denota a média populacional. Sabendo que P(Z < 1,645) = 0,95, em que Z é uma variável aleatória normal padrão, assinale a opção correta.
Para um estudo sobre o número de filhos em famílias de comunidades ribeirinhas do Amazonas, foi conduzido um planejamento amostral da seguinte forma: sortearam-se ao acaso duas comunidades ribeirinhas dentre todas do Amazonas, e foram registrados os números de filhos de todas as famílias das duas comunidades assim selecionadas.
Tal planejamento amostral é denominado na Estatística como amostragem
Um fabricante de carros elétricos concede garantia da bateria por 10 anos. Decorrido esse prazo, dos 10 mil carros vendidos, nenhum carro apresentou defeito na bateria.
A conclusão a que se pode chegar com base na ciência estatística é:
Considere que um pesquisador deseje estimar a média populacional de uma variável de interesse mediante amostragem aleatória simples com reposição. Nesse caso, para que o erro padrão da média amostral seja igual a 4% do desvio padrão populacional dessa variável de interesse, o tamanho da amostra deverá ser igual a
A equação y = mx + b, com m = 2,09 e b = 0,257, foi obtida na calibração de um método para a determinação cromatográfica de isoctano em misturas de hidrocarbonetos. Nessa equação, o eixo x apresenta valores de concentração de isoctano, em porcentagem molar, e o eixo y, a área sob o pico cromatográfico, em uma unidade arbitrária.
Tendo como referência as informações precedentes, julgue os itens subsecutivos, a respeito de fundamentos de estatística.
Se uma determinada amostra de hidrocarbonetos analisada pelo referido método apresenta um valor y igual a 2,65 unidades arbitrárias, então a porcentagem molar de isoctano nessa amostra é inferior a 1,5%.
A técnica de amostragem por amostra aleatória simples envolve:
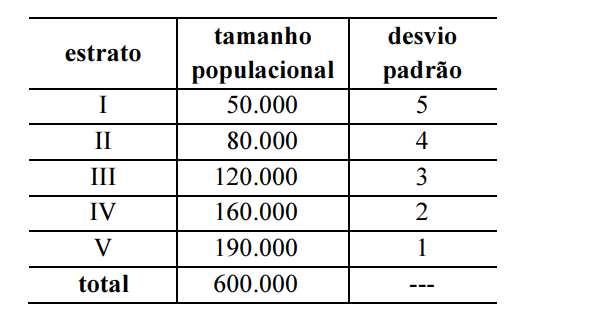
Suponha que uma população formada por 600 mil pessoas se encontre distribuída em cinco estratos, conforme o quadro precedente, que mostra, ainda, o desvio padrão da variável de interesse. Para a estimação da média populacional dessa variável de interesse mediante amostragem estratificada com alocação
ótima de Neyman, o estrato que deve contribuir com o maior número de unidades amostrais é o
Um estatístico precisa estimar a quantidade média de processos administrativos com 99% de confiança. Assuma que o desvio padrão é conhecido e igual a 10 processos, e que a margem de erro aceita é de 1 processo. O menor tamanho amostral que ele deve usar é de, aproximadamente:

De acordo com o último levantamento do Departamento de Recursos Humanos da Agência Beta, localizada em Vitória, o Banco Dubai que tem diversas agências localizadas no Brasil e em outros Países, conta com uma equipe de 686.791 funcionários, dos quais 35.777 têm idade entre 26 e 29 anos. Uma pesquisa direcionada para esse recorte de funcionários deseja estimar a porcentagem daqueles que avaliam positivamente o Plano de Cargos e Salários do Banco Dubai. Nesse caso hipotético, o tamanho aproximado da amostra aleatória simples que garantirá um erro amostral não superior a 5% deverá ser aproximadamente de
Um estudo acerca da saúde mental de detentos foi efetuado em determinada penitenciária que reúne 2 mil detentos acomodados em 100 celas. O levantamento dos dados foi conduzido da seguinte forma: dez celas foram selecionadas mediante sorteio aleatório, e todos os 193 detentos encontrados nessas celas foram entrevistados por uma equipe psicossocial.
No levantamento amostral da situação hipotética apresentada, a técnica de amostragem empregada foi a
Um exemplo de método de amostragem não probabilístico é a amostragem:
Considere a seguinte amostra aleatória simples:
2, 5, 5, 6, 6, 7, 7, 10.
A variância amostral que corresponde à estimativa não tendenciosa da variância populacional é aproximadamente igual a
O menor tamanho da amostra aleatória simples para que possamos garantir, com 99% de confiança, que a proporção de sucessos amostral não diferirá da proporção de sucessos populacional por mais de 1% deve ser aproximadamente igual a
[dado: se Z ~N(0, 1), P[ Z < 2,58] = 0,995]
Um Tribunal de Justiça deseja obter uma amostra de tamanho 3.000 de uma população de 60.000 ações. Esse Tribunal possui um cadastro em que cada ação está associada, sequencialmente, a um número (começando com o número 1 e terminando com o número 60.000).
De posse do referido cadastro e considerando o tamanho da amostra solicitada, o pesquisador utilizou o seguinte procedimento para a seleção da amostra:
1. Determinou o intervalo de seleção da amostra dividindo o total da população pelo tamanho da amostra: 60.000/3.000=20;
2. Elegeu aleatoriamente um número inteiro, entre [1, 20]. Essa foi a primeira ação selecionada;
3. A próxima ação selecionada foi definida pela soma do intervalo de seleção ao número selecionado na etapa 2.
E, assim, sucessivamente, foram determinados os próximos elementos, acrescentando-se ao selecionado anteriormente o intervalo de seleção da amostra.
O número escolhido na etapa de número 2 foi 17; logo, a primeira ação selecionada foi a de número 17; a seguinte, a de número 37, seguida da de número 57, e assim sucessivamente.
O milésimo elemento selecionado nessa amostra foi a ação de número:

