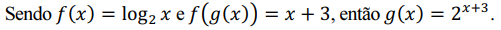Carmen, Heitor e Joana foram a um mesmo supermercado varejista e adquiriram os mesmos produtos alimentícios, quais sejam: arroz integral, feijão preto e farinha de mandioca, considerando as mesmas marcas e características. Carmen comprou 3 kg de feijão, 4 kg de arroz e 2 kg de farinha, pagando um total de R$ 73,50; Heitor adquiriu 3 kg de feijão, 5 kg de arroz e 2 kg de farinha, totalizando R$ 81,00; enquanto Joana pagou R$ 57,00 pelo conjunto de 3 kg de feijão, 3 kg de arroz e 1 kg de farinha. Se x, y e z são os preços (por quilo) de cada um dos produtos, então, a soma x + y + z é igual a
Em uma das sedes da Adapar há 4 amostras de fertilizantes em quantidades distintas de unidades. A respeito dessas amostras, sabe-se
que:
• a amostra A tem mais unidades do que a amostra B;
• a amostra C tem menos unidades do que a amostra D;
• a amostra D tem mais unidades do que a amostra B.
Com essas informações, conclui-se obrigatoriamente que
Um número X de servidores da Adapar participaram dos treinamentos A, B e C da seguinte maneira:
• 56 servidores participaram do treinamento A;
• 48 servidores participaram do treinamento B;
• 61 servidores participaram do treinamento C;
• 21 participaram dos treinamentos A e B;
• 25 participaram dos treinamentos A e C;
• 23 participaram dos treinamentos B e C;
• 12 participaram dos 3 treinamentos.
Sabendo que cada um dos X servidores participou de pelo menos um treinamento, assinale a alternativa que representa o número X.
O tempo para que uma unidade do corpo de bombeiros, após ser contatada, chegue a determinado setor da cidade é sempre um valor t (em minutos) que pertence ao domínio da
Nessa situação, caso a referida unidade do corpo de bombeiros se desloque para esse setor da cidade, o tempo, em minutos, será um
valor entre
Em uma escola, há 40 alunos que praticam futebol, 30 alunos que praticam vôlei e 15 alunos que praticam ambos os esportes. O número total de alunos que praticam pelo menos um desses esportes é
Texto 1A3
O governo estadual iniciou uma campanha publicitária com o intuito de informar a população a respeito do problema das ligações de ocorrências falsas para serviços de emergência oferecidos pelo SAMU e pelo corpo de bombeiros. Durante o ano em que a campanha foi veiculada, observou-se considerável redução no número de ocorrências falsas, fato que resultou em economia de recursos públicos. Os gastos relacionados à campanha em cada mês e o valor referente à economia de recursos públicos são descritos, respectivamente, pelas funções 
, em que 
são dados em milhões de reais e 
corresponde a primeiro de janeiro, 
, a primeiro de fevereiro e assim sucessivamente.
Em relação à situação apresentada no texto 1A3, é correto afirmar que o gasto máximo do governo estadual com a campanha ocorreu
Sobre dois números inteiros X e Y sabe-se que: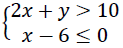
O valor mínimo de Y é:
Simplificando a expressão √1764: √7 + √70 . √10 - √1575, obtemos:
Para um evento que ocorrerá em Belo Horizonte, capital de Minas Gerais, o 1° Tenente do Corpo de Bombeiros de Minas Gerais precisa dimensionar a sua equipe. Dos 8 oficiais disponíveis para o trabalho serão escolhidos apenas 5.
Nesse contexto, assinale a alternativa que apresenta CORRETAMENTE a quantidade de grupos de oficiais que podem ser formados, sabendo-se que os oficiais terão funções idênticas.
Quando Mariana parou para abastecer seu veículo, o
indicador de combustível estava abaixo de 1/4 , mas ainda
fora da “reserva”, que tem 6 L. Nesse dia, o litro do etanol
estava custando R$ 3,99 e Mariana pediu ao frentista que
abastecesse seu veículo com R$ 100,00 desse combus-
tível. Considerando que o tanque do veículo de Mariana
tem capacidade para 60 L, após o abastecimento, o indi-
cador de combustível do carro dela deverá estar
A soma das raízes da equação x (x −1) • (x + 3) • (x 16) 2 + = 0 é
Sabendo-se que o desvio padrão de X é 9, a variância de 3X + 12 é:
Um acidente envolvendo um poste de distribuição de energia elétrica causou, em uma comunidade, um blecaute que durou exatamente 2,17 horas.
Nessa situação hipotética, a duração do referido blecaute equivale a
Seja x um número positivo. Se a média aritmética de (x + 1)2 e (x − 1)2 é igual a 10, então o valor de x é:
