Considerando a técnica de amostragem aleatória simples, as variáveis contínuas Y e X e o estimador de regressão linear (de Y em X) da média de Y, denotado por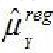 
, analise.
I. O estimador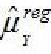 
envolve um termo de correção que depende da estimativa do coeficiente angular da regressão de Y em X.
II. A estimativa da variância do estimador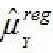 
é alterada pelo sinal (negativo ou positivo) da estimativa do coeficiente de correlação linear entre Y e X.
III. O vício (ou viés) do estimador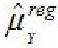 
é zero, mesmo se o coeficiente de correlação linear entre as variáveis Y e X for diferente de zero.
Assinale
Um estudo tem como objetivo deduzir um modelo que permite encontrar uma relação linear, sem intercepto, entre duas variáveis X e Y com base em 20 observações. O modelo foi definido como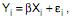 
em que:
I.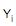 
é uma variável aleatória e representa o valor da variável dependente na i-ésima observação.
II.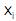 
é o valor da variável explicativa na i-ésima observação.
III. 
é o erro aleatório com as respectivas hipóteses consideradas para a regressão linear simples.
IV. ß é o parâmetro do modelo, cuja estimativa foi obtida pelo método dos mínimos quadrados.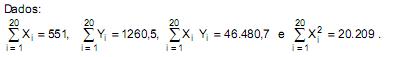 
Utilizando a equação da reta encontrada pelo método dos mínimos quadrados, obtém-se que o valor de Y, quando X for igual a 50, é
A matriz A = (a ij ) a seguir indica a quantidade de grãos (em toneladas) produzidas nas fazendas i nos meses j, i = 1,..., 5, j = 1, ...,4.
As cinco fazendas fazem parte de uma mesma cooperativa. O mês em que a cooperativa mais produziu foi o:
