Uma amostra aleatória de tamanho 100 de uma distribuição
normal com média μ desconhecida e variância 100, será
observada para testar H0 : μ≤ 22 versus H1: μ> 22
O teste uniformemente mais poderoso de tamanho α = 0,05
rejeitará a hipótese nula se o valor da média amostral for
Uma variável aleatória X tem função de distribuição acumulada
dada por:

A probabilidade P[ 1,2 ≤ X < 3 ] é igual a
2% das mulheres de uma população muito grande têm uma certa
síndrome.
Considere o experimento de se selecionar mulheres
aleatoriamente até que uma que tenha a síndrome seja sorteada.
Se X é o número de mulheres selecionadas, então o valor
esperado de X é igual a
Os pesos de determinados componentes são normalmente
distribuídos. Para estimar a média desses pesos, uma amostra
aleatória x1 , x2 , ..., x36 , de tamanho 36, foi observada e mostrou
os seguintes resultados:
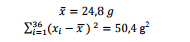
Um intervalo de 95% de confiança para a média será dado,
aproximadamente, por
Para testar, ao nível de significância de 5%, a hipótese nula de
independência ente dois atributos A e B a seguinte tabela de
contingências foi observada:
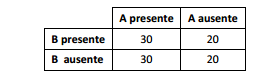
O valor da estatística qui–quadrado usual, a ser comparada com o
95% percentil da distribuição qui–quadrado com 1 grau de
liberdade (que é igual a 3,841) é igual a _____ e a decisão
é _____.
As lacunas ficam corretamente preenchidas por:
Suponha que X1 , X2 , ..., Xn seja uma amostra aleatória de uma
distribuição Poisson com parâmetro γdesconhecido (γ> 0) e que
a distribuição a priori de γ seja uma distribuição gama (α β).
Assinale a opção que indica a distribuição a posteriori de γ , dado
que Xi = xi, i = 1, ..., n .
Avalie se as distribuições a seguir pertencem à família
exponencial de distribuições:
I. Normal (μ, σ2)
II. Binomial(n, p)
III. Poisson(γ)
IV. Uniforme (0, θ)
Pertencem à família exponencial
Suponha que A e B sejam dois eventos independentes, com probabilidades positivas. A esse respeito, assinale V para a afirmativa verdadeira e F para a falsa.
( ) A e B não podem ser mutuamente exclusivos.
( ) Se P[A] = 0,8 então P[B] não pode ser maior do que 0,5
( ) P[A|B] = P[A].
As afirmativas são, respectivamente,
Uma variável aleatória X tem média 4 e desvio padrão igual a 2
Se Y = 3X – 2 então a média e o desvio padrão de Y são,
respectivamente,
Uma urna contém n (n > 3) bolas numeradas 1, 2, ..., n. Se três
bolas são retiradas da urna com reposição, a probabilidade de
que as três bolas tenham números diferentes é igual a:
Uma variável aleatória populacional tem variância igual a 25. Se
uma amostra aleatória simples de tamanho 100 for obtida, a
probabilidade de que o valor da média amostral não difira do da
média populacional por mais de 0,5 é, aproximadamente, igual a
Para testar a hipótese nula de que a média de uma distribuição
normal não é maior do que 20, uma amostra aleatória de
tamanho 25 foi observada e indicou: x= 22,4 e s2 = 16
O p–valor associado a esses dados é tal que
Os experimentos fatoriais são muito usados em experimentos
envolvendo vários fatores para os quais é necessário estudar o
efeito conjunto dos fatores sobre a resposta. O caso especial mais
importante do experimento fatorial geral é o de k fatores, cada
um com 2 níveis.
Em relação a esse caso especial, assinale V para a afirmativa
verdadeira e F para falsa.
I. Os níveis têm de ser quantitativos.
II. O plano 2k é particularmente útil nos estágios iniciais do
trabalho experimental, quando poucos fatores devem ser
investigados.
III. Ele fornece o menor número de realizações com o qual k
fatores podem ser simultaneamente investigados em um
planejamento fatorial completo.
As afirmativas são, respectivamente,

