Pretende-se usar um modelo de regressão linear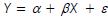 
para ajustar n pares de valores observados 
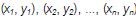. Supõe-se que os erros 
tenham média 0, sejam normalmente distribuídos, todos com mesma variância, e sejam não correlacionados. Se a e b são as estimativas de mínimos quadrados de 
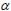e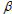 
, respectivamente, avalie as afirmativas a seguir:
I. As estimativas de mínimos quadrados de ?? e ?? são os valores de a e b que resolvem as equações normais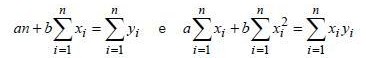 
II. a e b são estimadores não viesados 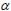de e de 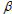, respectivamente.
III. O coeficiente de determinação, R², mede a porcentagem da variância total dos valores y's que é explicada pela regressão e, desse modo, quanto maior o valor do coeficiente de determinação, melhor é o ajuste do modelo.
Assinale:
Os dados a seguir são as quantidades de empregados de cinco pequenas empresas: 6, 5, 8, 5, 6. A variância da quantidade de empregados dessas cinco empresas é igual a:
Em relação à distribuição normal, assinale a afirmativa incorreta.
Para testar a hipótese de que uma média populacional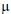 
de uma variável normalmente distribuída com variância igual a 64 é maior do que 200, uma amostra aleatória simples de tamanho 100 será observada. Ao nível de significância de 5%, o critério de decisão usual estabelece que a hipótese nula de que 
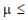100 deve ser rejeitada se o valor observado da média amostral for:
