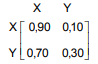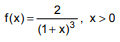De um histograma e uma tabela de frequências absolutas, elaborados para analisar a distribuição dos salários dos empregados em uma empresa, obtém-se a informação que 24 empregados ganham salários com valores pertencentes ao intervalo (2.000; 4.000], em reais, que apresenta uma densidade de frequência de 0,75 × 10−4(R$)−1.
Densidade de frequência de um intervalo é o resultado da divisão da respectiva frequência relativa pela amplitude deste intervalo. Em um intervalo do histograma que está sendo analisado, com uma amplitude de R$ 3.000,00 e uma densidade de frequência de 1 × 10−4(R$)−1, tem-se que o correspondente número de empregados é igual a
Analisando uma curva de frequência de uma distribuição estatística, observa-se que ela: I. é unimodal. II. apresenta a moda menor que a mediana e a mediana menor que a média. III. possui os dados da distribuição fortemente concentrados em torno da moda. Então, essa distribuição
Uma variável aleatória X tem a seguinte função de densidade:
Deseja-se obter, utilizando o método da máxima verossimilhança, a estimativa do parâmetro K, sabendo-se que da população correspondente de X foi extraída uma amostra aleatória, com reposição de 4 observações independentes, ou seja: (0,50; 0,70; 0,80; 0,72).
Obs.: Se ln(a) é o logaritmo neperiano de a então: ln(0,50) = −0,69, ln(0,70) = −0,36, ln(0,80) = −0,22 e ln(0,72) = −0,33.
A estimativa encontrada para K, com base na amostra, foi de
Em uma determinada data, o gerente comercial de uma fábrica de um produto marca X, concorrente somente com o produto de outro fabricante marca Y, insatisfeito com a participação de seu produto no mercado, decide fazer uma promoção de seu produto. Verifica então que com a promoção, mensalmente, 90% dos clientes que consumiam X continuaram a consumir X e 70% dos que consumiam Y passaram a consumir X. Seja a matriz de transição T abaixo:
Se o gerente ao longo do tempo não interrompe a promoção, então a matriz estacionária S correspondente à matriz de transição T é igual a
Uma cidade sede do interior possui três varas trabalhistas. A 1ª Vara comporta 50% das ações trabalhistas, a 2ª Vara comporta 30% e a 3ª Vara as 20% restantes. As porcentagens de ações trabalhistas oriundas da atividade agropecuária são 3%, 4% e 5% para a 1ª , 2ª e 3ª Varas, respectivamente. Escolhe-se uma ação trabalhista aleatoriamente e constata-se ser originária da atividade agropecuária. A probabilidade dessa ação ser da 1ª Vara trabalhista é, aproximadamente:
Uma pesquisa piloto realizada no setor de embalagens, referente aos motivos de demissão de funcionários, mostra que 34% dos casos de demissão, p*, tem como motivo a situação financeira da empresa. Utilizando um nível de confiança de 95%, a proporção p* obtida na pesquisa piloto, com uma margem de erro amostral e ≤ 3% e que P(Z ≥ 1,96) = 2,5%, o tamanho mínimo necessário da amostra para estimar a proporção de demissões causadas por motivos financeiros, no setor de embalagens, nas condições estipuladas é
Pode-se demonstrar que se X for uma variável aleatória contínua com função densidade de probabilidade f(x) e função de densidade acumulada F(x), então a variável aleatória U = F(x) tem distribuição uniforme no intervalo [0,1]. Considere uma variável aleatória Y com uma distribuição exponencial com média 0,5.
Foram simulados três valores de uma distribuição uniforme com o seguinte resultado: u1 = 0,66; u2 = 0,42; u3 = 0,18.
Dado que In(0,34) = −1,79; In(0,58) = −0,545; In(0,82) = −0,2 e utilizando as informações disponíveis, é possível gerar três valores da variável aleatória Y. A soma aproximada desses três valores gerados é
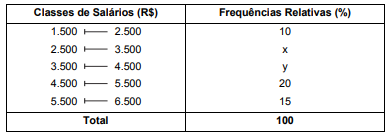
Seja a tabela de frequências relativas abaixo correspondendo à distribuição dos salários dos funcionários sem nível superior, lotados em um órgão público. Para o segundo e terceiro intervalos de classes não foram fornecidas as respectivas frequências (na tabela, denotadas por x e y, respectivamente).
Utilizando o método da interpolação linear, obteve-se o valor de R$ 3.900,00 para a mediana (Md) dos salários. O valor da média aritmética (Me) foi obtido considerando que todos os valores incluídos em um certo intervalo de classe são coincidentes com o ponto médio deste intervalo. A expressão (3Md − 2Me) apresenta, em R$, um valor igual a
Com base em uma amostra aleatória de tamanho 12 obtiveram-se, pelo método dos momentos, as estimativas pontuais dos parâmetros a e b de uma variável aleatória X uniformemente distribuída no intervalo (a, b), sendo 0 < a < b. A média amostral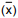 
apresentou um valor igual a 1,5 e a amplitude do intervalo encontrado foi igual a 6. O segundo momento, não centrado, referente à amostra foi igual a
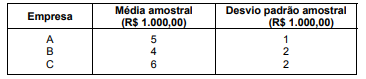
Um determinado ramo de atividade é composto por 3 empresas (A, B e C) independentes. Um estudo é realizado para comparar os salários, em R$ 1.000,00, dos empregados de A, B e C, sabendo-se que não existe alguém trabalhando em mais de uma empresa. Uma amostra aleatória, com reposição, de 24 empregados, sendo 8 de cada uma das empresas citadas, foi retirada da população de empregados desse ramo de atividade. Na tabela abaixo, verifica-se os salários médios e os respectivos desvios padrões amostrais (obtidos por meio de estimadores não viciados das variâncias populacionais) observados para cada uma das amostras.
Se k é o valor da estatística F (F calculado) utilizado para testar a igualdade das médias populacionais dos salários dos empregados em A, B e C obtém-se que
Os sinistros de uma companhia de seguros (em R$ milhões) são modelados por uma variável aleatória contínua X com função densidade de probabilidade dada por:
A probabilidade de um sinistro, aleatoriamente escolhido, exceder R$ 1,5 milhões é
O expediente de uma Vara Trabalhista recebe, em média, 5 reclamações por hora seguindo um processo de Poisson. O expediente tem apenas um funcionário com tempo de atendimento segundo uma distribuição exponencial de média 1/3 de hora. Suponha que o processo de chegada das reclamações e o tempo de atendimento do funcionário sejam independentes e que o expediente se encontra vazio. Um advogado acaba de chegar ao expediente e o funcionário começa o atendimento. A probabilidade de o advogado ser atendido antes de chegar o próximo reclamante é
Considere o processo de média móvel de ordem, MA(1) escrito da forma:
X t = θ0 + εt + θ1εt−1 para t = 1,2,3,... e εt uma sequência de variáveis aleatórias independentes e identicamente distribuídas com E(εt) = 0 e var(εt) = σ2.
A média e a variância de Xt são, respectivamente:
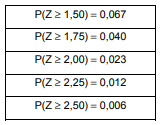
No período de 81 dias úteis, foram coletadas informações sobre o fluxo de conciliações em um Tribunal Regional do Trabalho. Considere que diariamente são realizados, em média, 64 acordos de conciliação no Tribunal segundo uma distribuição de Poisson. Usando o Teorema Central do Limite, pode-se considerar que a média diária da amostra de 81 dias terá uma distribuição aproximadamente normal. Considere, abaixo, a tabela referente à distribuição normal padrão, Z:
Com base nessa aproximação e os dados fornecidos, a probabilidade de que a média amostral da amostra de 81 dias seja superior a 66 conciliações é, em %, igual a
Os estimadores independentes e não viesados E 1, E2 e E3 são utilizados para a média μ de uma população normalmente distribuída e desvio padrão igual a 0,5. Tem-se que E1 = mX1 + nX2 − 2pX3, E2 = mX1 + 2nX2 − 4pX3 e E3 = 2mX1 + nX2 − 3pX3 sendo (X1, X2, X3) uma amostra aleatória simples com reposição da população e m, n e p parâmetros reais tal que n=2m=2p. Entre esses 3 estimadores, o mais eficiente apresenta uma variância igual a
