Visando a melhoria estética de um veículo, o vendedor de uma loja sugere ao consumidor que ele troque as rodas de seu automóvel de aro 15 polegadas para aro 17 polegadas, o que corresponde a um diâmetro maior do conjunto roda e pneu.
Duas consequências provocadas por essa troca de aro são:
Muitos primatas, incluindo nós humanos, possuem visão tricromática: têm três pigmentos visuais na retina sensíveis à luz de uma determinada faixa de comprimentos de onda. Informalmente, embora os pigmentos em si não possuam cor, estes são conhecidos como pigmentos “azul", “verde" e “vermelho" e estão associados à cor que causa grande excitação (ativação). A sensação que temos ao observar um objeto colorido decorre da ativação relativa dos três pigmentos. Ou seja, se estimulássemos a retina com uma luz na faixa de 530 nm (retângulo I no gráfico), não excitaríamos o pigmento “azul", o pigmento “verde" seria ativado ao máximo e o “vermelho" seria ativado em aproximadamente 75%, e isso nos daria a sensação de ver uma cor amarelada. Já uma luz na faixa de comprimento de onda de 600 nm (retângulo II) estimularia o pigmento “verde" um pouco e o “vermelho" em cerca de 75%, e isso nos daria a sensação de ver laranja-avermelhado. No entanto, há características genéticas presentes em alguns indivíduos, conhecidas coletivamente como Daltonismo, em que um ou mais pigmentos não funcionam perfeitamente.
Caso estimulássemos a retina de um indivíduo com essa característica, que não possuísse o pigmento conhecido como “verde", com as luzes de 530 nm e 600 nm na mesma intensidade luminosa, esse indivíduo seria incapaz de
Talvez você já tenha bebido suco usando dois canudinhos iguais. Entretanto, pode-se verificar que, se colocar um canudo imerso no suco e outro do lado de fora do líquido, fazendo a sucção simultaneamente em ambos, você terá dificuldade em bebê-lo.
Essa dificuldade ocorre porque o(a)
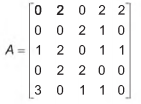
A Transferência Eletrônica Disponível (TED) é uma transação financeira de valores entre diferentes bancos. Um economista decide analisar os valores enviados por meio de TEDs entre cinco bancos (1,2, 3, 4 e 5) durante um mês. Para isso, ele dispõe esses valores em uma matriz A = [aij], em que 1 ≤ i ≤ 5 e 1 ≤ j ≤ 5, e o elemento aij corresponde ao total proveniente das operações feitas via TED, em milhão de real, transferidos do banco i para o banco j durante o mês. Observe que os elementos aij= 0, uma vez que TED é uma transferência entre bancos distintos. Esta é a matriz obtida para essa análise:
Com base nessas informações, o banco que transferiu a maior quantia via TED é o banco
A prefeitura de um pequeno município do interior decide colocar postes para iluminação ao longo de uma estrada retilínea, que inicia em uma praça central e termina numa fazenda na zona rural. Como a praça já possui iluminação, o primeiro poste será colocado a 80 metros da praça, o segundo, a 100 metros, o terceiro, a 120 metros, e assim sucessivamente, mantendo-se sempre uma distância de vinte metros entre os postes, até que o último poste seja colocado a uma distância de 1 380 metros da praça.
Se a prefeitura pode pagar, no máximo, R$ 8 000,00 por poste colocado, o maior valor que poderá gastar com a colocação desses postes é
Uma empresa deseja iniciar uma campanha publicitária divulgando uma promoção para seus possíveis consumidores. Para esse tipo de campanha, os meios mais viáveis são a distribuição de panfletos na rua e anúncios na rádio local. Considera-se que a população alcançada pela distribuição de panfletos seja igual à quantidade de panfletos distribuídos, enquanto que a alcançada por um anúncio na rádio seja igual à quantidade de ouvintes desse anúncio. O custo de cada anúncio na rádio é de R$ 120,00, e a estimativa é de que seja ouvido por 1 500 pessoas. Já a produção e a distribuição dos panfletos custam R$ 180,00 cada 1 000 unidades. Considerando que cada pessoa será alcançada por um único desses meios de divulgação, a empresa pretende investir em ambas as mídias.
Considere X e Y os valores (em real) gastos em anúncios na rádio e com panfletos, respectivamente.
O número de pessoas alcançadas pela campanha será dado pela expressão
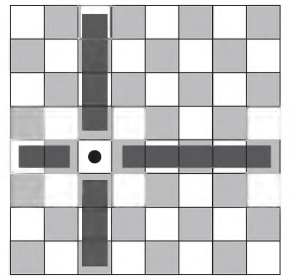
Um designer de jogos planeja um jogo que faz uso de um tabuleiro de dimensão n x n, com n > 2 , no qual cada jogador, na sua vez, coloca uma peça sobre uma das casas vazias do tabuleiro. Quando uma peça é posicionada, a região formada pelas casas que estão na mesma linha ou coluna dessa peça é chamada de zona de combate dessa peça. Na figura está ilustrada a zona de combate de uma peça colocada em uma das casas de um tabuleiro de dimensão 8 x 8.
O tabuleiro deve ser dimensionado de forma que a probabilidade de se posicionar a segunda peça aleatoriamente, seguindo a regra do jogo, e esta ficar sobre a zona de combate da primeira, seja inferior a 1/5.
A dimensão mínima que o designer deve adotar para esse tabuleiro é
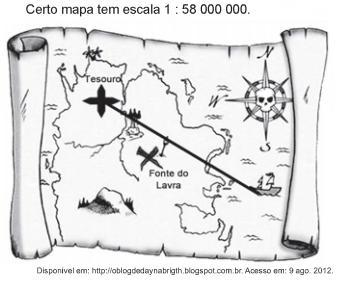
Um mapa é a representação reduzida e simplificada de uma localidade. Essa redução, que é feita com o uso de uma escala, mantém a proporção do espaço representado em relação ao espaço real.
Considere que, nesse mapa, o segmento de reta que liga o navio à marca do tesouro meça 7,6 cm.
A medida real, em quilômetro, desse segmento de reta é
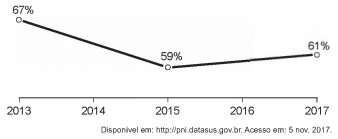
A raiva é uma doença viral e infecciosa, transmitida por mamíferos. A campanha nacional de vacinação antirrábica tem o objetivo de controlar a circulação do vírus da raiva canina e felina, prevenindo a raiva humana. O gráfico mostra a cobertura (porcentagem de vacinados) da campanha, em cães, nos anos de 2013, 2015 e 2017, no município de Belo Horizonte, em Minas Gerais. Os valores das coberturas dos anos de 2014 e 2016 não estão informados no gráfico e deseja-se estimá-los. Para tal, levou-se em consideração que a variação na cobertura de vacinação da campanha antirrábica, nos períodos de 2013 a 2015 e de 2015 a 2017, deu-se de forma linear.
Qual teria sido a cobertura dessa campanha no ano de 2014?
Considere 0,30 como aproximação para log102.
Em que ano a empresa atingiu ou atingirá a densidade de 100 bilhões de transistores?
O salto ornamental é um esporte em que cada competidor realiza seis saltos. A nota em cada salto é calculada pela soma das notas dos juízes, multiplicada pela nota de partida (o grau de dificuldade de cada salto). Fica em primeiro lugar o atleta que obtiver a maior soma das seis notas recebidas.
O atleta 10 irá realizar o último salto da final. Ele observa no Quadro 1, antes de executar o salto, o recorte do quadro parcial de notas com a sua classificação e a dos três primeiros lugares até aquele momento.
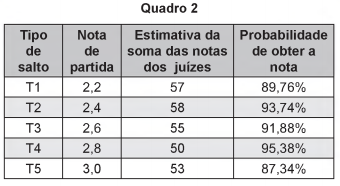
Ele precisa decidir com seu treinador qual salto deverá realizar. Os dados dos possíveis tipos de salto estão no Quadro 2.
O atleta optará pelo salto com a maior probabilidade de obter a nota estimada, de maneira que lhe permita alcançar o primeiro lugar.
Considerando essas condições, o salto que o atleta deverá escolher é o de tipo
Ao organizar as informações, no processo de construção do texto, o autor estabelece sua intenção comunicativa. Nesse poema, Gregório de Matos explora os ditados populares com o objetivo de
Para combater a falta de civismo, a polícia da cidade de Barcelona tem
O artista francês Pierre David, ao evidenciar seu encantamento com a diversidade de cores de peles no Brasil, no projeto Nuancier, também
Tendo em vista a procura por atividades de lazer em períodos de recesso escolar, esse fôlder