Uma população com uma certa quantidade de elementos é dividida previamente em grupos mutuamente exclusivos e dentro dos quais são sorteadas amostras casuais simples. Esse tipo de amostragem é denominado de Amostragem
Para realizar uma pesquisa, um estudante deseja estimar a proporção populacional, extraindo uma amostra, usando como estimador a proporção amostral. Com o erro máximo tolerado de 2% e com o grau de confiança de 95%. Qual deverá ser o tamanho da amostra, tomando o valor máximo para proporções.
Sabendo que F(z) é a função de distribuição acumulada da normal padrão, onde F(1,3) ≅ 0,90, F(1,64) ≅ 0,95 F(1,96) ≅ 0,975, F(2,58) = 0,995
Nos processos de controle, o objetivo fundamental da amostragem estatística consiste em
Uma população de tamanho 1.600 é dividida em 80 subpopulações distintas. Por meio de um sorteio, 20 subpopulações são selecionadas e todos os elementos nas subpopulações selecionadas são observados. Este tipo de amostragem é denominado de Amostragem
A respeito do total amostral Tn = X1 + X2 + ... + Xn, em que X1, X2, ..., Xn é uma amostra aleatória simples retirada de uma distribuição gama com média µ e desvio padrão σ, julgue o próximo item.
O valor esperado do total amostral Tn é igual a µ.
Tendo em vista que a abordagem da população sobre o conjunto de unidades amostrais pode ser aleatória, sistemática ou mista, e que, entre esses arranjos estruturais, situam-se os processos de amostragem mais usuais em inventários florestais — amostragem aleatória simples, amostragem estratificada, amostragem sistemática, amostragem em dois estágios e amostragem em conglomerados —, julgue o próximo item, relativo a esses processos de amostragem.
A amostragem em dois estágios é incluída entre os processos aleatórios irrestritos, pois, nessa amostragem, o segundo estágio pode ocorrer independentemente do primeiro.
A seleção amostral pode ser feita, em geral, por dois métodos. As amostras podem ser probabilísticas e não probabilísticas. No caso de amostras não probabilísticas há uma preocupação com a representatividade, mas sem garantias da aleatoriedade.
Sobre esse tipo de seleção, é correto afirmar que:
Um estudo acerca do tempo (x, em anos) de guarda de autos findos em determinada seção judiciária considerou uma amostragem aleatória estratificada. A população consiste de uma listagem de autos findos, que foi segmentada em quatro estratos, segundo a classe de cada processo (as classes foram estabelecidas por resolução de autoridade judiciária). A tabela a seguir mostra os tamanhos populacionais (
N) e amostrais (n), a média amostral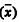 
e a variância amostral dos tempos (s2) correspondentes a cada estrato.
Considerando que o objetivo do estudo seja estimar o tempo médio populacional (em anos) de guarda dos autos findos, julgue o item a seguir.
No desenho amostral em tela há duas unidades amostrais: a primeira (unidade primária) corresponde à classe de cada processo, e a segunda (unidade secundária) refere-se a auto findo presente na listagem
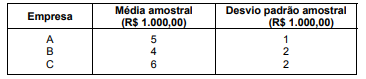
Um determinado ramo de atividade é composto por 3 empresas (A, B e C) independentes. Um estudo é realizado para comparar os salários, em R$ 1.000,00, dos empregados de A, B e C, sabendo-se que não existe alguém trabalhando em mais de uma empresa. Uma amostra aleatória, com reposição, de 24 empregados, sendo 8 de cada uma das empresas citadas, foi retirada da população de empregados desse ramo de atividade. Na tabela abaixo, verifica-se os salários médios e os respectivos desvios padrões amostrais (obtidos por meio de estimadores não viciados das variâncias populacionais) observados para cada uma das amostras.
Se k é o valor da estatística F (F calculado) utilizado para testar a igualdade das médias populacionais dos salários dos empregados em A, B e C obtém-se que
Os estimadores independentes e não viesados E 1, E2 e E3 são utilizados para a média μ de uma população normalmente distribuída e desvio padrão igual a 0,5. Tem-se que E1 = mX1 + nX2 − 2pX3, E2 = mX1 + 2nX2 − 4pX3 e E3 = 2mX1 + nX2 − 3pX3 sendo (X1, X2, X3) uma amostra aleatória simples com reposição da população e m, n e p parâmetros reais tal que n=2m=2p. Entre esses 3 estimadores, o mais eficiente apresenta uma variância igual a
Acerca da amostragem estratificada, analise as afirmativas a seguir.
I. Visa a produzir estimativas mais precisas, produzir estimativas para a população toda e para subpopulações.
II. Em geral, quanto menos os elementos de cada estrato forem parecidos entre si e também entre os estratos, maior será a precisão dos estimadores.
III. A estratificação produz necessariamente estimativas mais eficientes do que a amostragem aleatória simples.
Está correto o que se afirma em
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
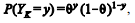
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, 
represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
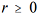
O amostrador de Gibbs, um algoritmo sequencial de Monte Carlo, permite simular a distribuição a priori do parâmetro θ, desde que a forma funcional da sua função de densidade, ƒ(θ), seja conhecida.
Considere uma amostragem aleatória simples de uma população de tamanho muito grande. O tamanho aproximado da amostra que permite estimar uma proporção Y, com margem de erro máxima de 0,05, a um nível de confiança de 90%, é
Suponha que uma amostra de tamanho n = 6 será extraída de uma população de 20 indivíduos, sendo a idade a variável de interesse. A população é mostrada na íntegra a seguir.
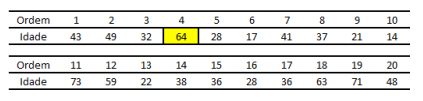
A extração seguirá a técnica de amostragem sistemática, iniciando pelo indivíduo de ordem 4, acima grifado.
Se o intervalo de seleção é igual a três, a estimativa não tendenciosa da média populacional será igual a:
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Nesse teste de hipóteses, comete-se o erro do tipo II caso a hipótese H0 seja rejeitada, quando, na verdade, H0 não deveria ser rejeitada.
