X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e 
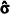representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
A soma X1 + X2 + ... + X10 é uma estatística suficiente para a estimação do parâmetro μ.
Analise a tabela de distribuição de frequência abaixo:
TABELA: anos de serviço na PM, militares do 185º BPM, dezembro de 2017:
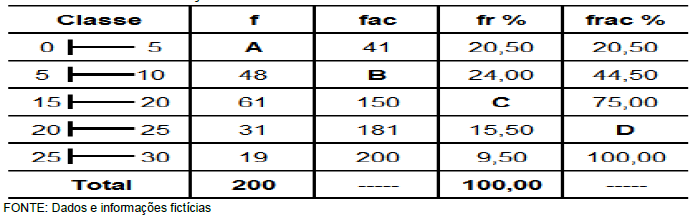
Sabe-se que f é a frequência absoluta, fac é a frequência absoluta acumulada, fr% é a frequência relativa (percentual) e frac% é a frequência relativa (percentual) acumulada. Considerando as informações da tabela, é CORRETO afirmar que os valores de A, B, C, D, são respectivamente:
Para o planejamento de uma pesquisa de campo, do ponto de vista estatístico, existem três aspectos fundamentais a definir, quais sejam: a população alvo, o modo de seleção e o tamanho da amostra.
Esses aspectos estão logicamente interligados e sobre eles é correto afirmar que:
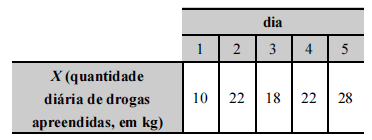
Tendo em vista que, diariamente, a Polícia Federal apreende uma quantidade X, em kg, de drogas em determinado aeroporto do Brasil, e considerando os dados hipotéticos da tabela precedente, que apresenta os valores observados da variável X em uma amostra aleatória de 5 dias de apreensões no citado aeroporto, julgue o próximo item.
A tabela em questão descreve a distribuição de frequências da quantidade de drogas apreendidas nos cinco dias que constituem a amostra.
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
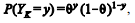
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, 
represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
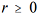
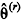
No algoritmo de Metropolis-Hastings tem-se a forma iterativa
, na qual ƒ representa a função de densidade a priori de θ, e 
> 0 representa um incremento aleatório. Nesse algoritmo, a probabilidade de aceitação do valor proposto 
como uma estimativa viável para o parâmetro de interesse é constante.
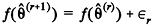
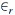
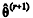
A respeito de um plano amostral com base na amostragem por conglomerados, assinale a alternativa correta.
Para obter uma amostra de tamanho 1.000 dentre uma população de tamanho 20.000, organizada em um cadastro em que cada elemento está numerado sequencialmente de 1 a 20.000, um pesquisador utilizou o seguinte procedimento:
I - calculou um intervalo de seleção da amostra, dividindo o total da população pelo tamanho da amostra: 20.000/1.000 = 20;
II - sorteou aleatoriamente um número inteiro, do intervalo [1, 20]. O número sorteado foi 15; desse modo, o primeiro elemento selecionado é o 15º;
III - a partir desse ponto, aplica-se o intervalo de seleção da amostra: o segundo elemento selecionado é o 35º (15+20), o terceiro é o 55º (15+40), o quarto é o 75º (15+60), e assim sucessivamente.
O último elemento selecionado nessa amostra é o
Sobre as vantagens da amostragem por conglomerados, avalie as afirmativas a seguir.
I. O plano amostral é mais eficiente já que dentro dos conglomerados os elementos tendem a ser mais parecidos.
II. Não há necessidade de uma lista de identificação dos elementos da população.
III. Tem, em geral, menor custo por elemento, principalmente quando o custo por observação cresce se aumenta a distância entre os elementos.
Está correto o que se afirma em
Uma amostra aleatória simples
Y1, Y2,..., Yn, retirada de uma população Bernoulli, é tal que
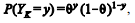
para
y = 0 ou 1, 0 < θ < 1 e k = 1, 2, ..., n. O objetivo é efetuar inferências acerca do parâmetro θ mediante aplicação de métodos computacionais.
Considerando que para
, represente a estimativa de θ obtida na r-ésima iteração de um algoritmo de estimação, julgue o seguinte item.
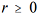
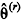
O método de Monte Carlo via cadeia de Markov (MCMC) pertence à classe de algoritmos de estimação não sequencial, em que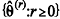 
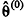
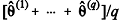
forma um conjunto de valores mutuamente independentes. Excluindo-se o valor inicial 
, uma estimativa do parâmetro θ é dada por 
, na qual q representa um valor suficientemente grande.
Deseja-se estimar o total de carboidratos existentes em um lote de 500.000 g de macarrão integral. Para esse fim, foi retirada uma amostra aleatória simples constituída por 5 pequenas porções desse lote, conforme a tabela seguinte, que mostra a quantidade x amostrada, em gramas, e a quantidade de carboidratos encontrada, y, em gramas.
Com base nas informações e na tabela apresentadas, julgue o item a seguir.
Considerando o estimador de razão, estima-se que existem 250.000 g de carboidratos nesse lote de macarrão integral.
Amostragem probabilística é considerada
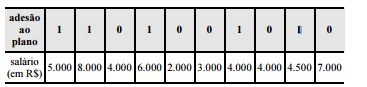
Considerando que os dados na tabela mostram salários de diferentes servidores que aderiram (1) ou não aderiram (0) a determinado plano de previdência complementar, julgue os itens subsecutivos.
Um modelo de regressão logística só aceita variáveis
categóricas; um modelo de regressão linear só aceita
variáveis quantitativas.
Considerando uma população finita em que a média da variável de
interesse seja desconhecida, julgue os itens a seguir.
Para uma amostra aleatória estratificada, quanto mais homogêneos forem os valores populacionais dentro de cada estrato, menor será o tamanho de amostra necessário para se obter determinado nível de precisão das estimativas da média populacional.
A variável X é do tipo qualitativo nominal.
A respeito de uma amostra de tamanho n = 10, com os valores amostrados {0,10, 0,06, 0,10, 0,12, 0,08, 0,10, 0,05, 0,15, 0,14, 0,11}, extraídos de determinada população, julgue os itens seguintes.
A estimativa pontual da média a partir dessa amostra é inferior a 0,09
