Em uma caixa, estão postas dez bolas de tênis, sendo cinco azuis e cinco amarelas. Sem olhar para dentro da caixa e sem ver as bolas, qual a probabilidade de uma pessoa retirar da caixa duas bolas amarelas?
Um dado de seis faces tem duas faces com o número 2, duas faces com o número 4 e duas faces com o número 6. Três rapazes, Jonas, Fábio e Rafael, jogaram esse dado algumas vezes, não necessariamente a mesma quantidade de vezes. Ao final desses lançamentos, verificou-se que:
- Jonas obteve face com número 2 em 1/3 dos seus lançamentos e face com número 6 nos demais.
- Rafael realizou cinco lançamentos, e o total de pontos obtidos por ele foi o menor possível;
- Fábio realizou a metade dos lançamentos de Jonas, obtendo face com número 4 em todos esses lançamentos.
- A soma dos pontos obtidos por Jonas, Fábio e Rafael foi 50.
Dessa forma, o total de lançamentos realizados pelos três rapazes é igual a:
O número de anagramas que podem ser formados com as letras da palavra DEMOCRACIA em que todas as vogais estejam juntas e todas as consoantes também estejam juntas é igual a
Em uma escola de ensino fundamental, a professora questionou cinco crianças sobre o sumiço do livro de um dos colegas. Quando foram questionadas, as crianças responderam:
- Foi a criança E, respondeu a criança A.
- Não fui eu, respondeu a criança B.
- A criança B está falando a verdade, respondeu a criança C.
- Foi a criança A, respondeu a criança D.
- A criança D está mentindo, respondeu a criança E.
Sabe-se que foi uma destas cinco crianças que escondeu o livro do colega e que uma delas está mentindo. Sendo assim, quem escondeu o livro do colega foi:
Um professor ensina numa mesma sala de aula, em dois turnos diferentes. A sala de aula possui 25 cadeiras, distribuídas conforme a figura. Entretanto, na turma A há um total de 20 alunos, enquanto na turma B há um total de 15 alunos.
Admitindo que todos os alunos ocupam as cadeiras sempre de forma aleatória e que, em ambas as turmas, há apenas um aluno por nome de “Pedro”, quais as chances dos dois “Pedros” sentarem em cadeiras da primeira fileira num mesmo dia?
Assinale a alternativa que mostra corretamente a negação lógica da frase “Todo estudante gosta de feriado”.
Considere a sequência de infinitos termos (8, 10, 70, 74, 690, 696, 6890, 6898,…), que segue um padrão definido pela posição em que cada elemento, do segundo em diante, se encontra. O décimo segundo elemento dessa sequência é
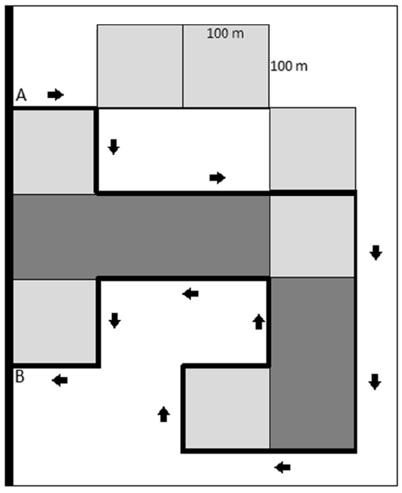
Considere que uma equipe da polícia tenha entrado na área descrita pela planta anterior para busca e apreensão de drogas. A planta é composta de 7 quadrados de mesma medida e 2 retângulos. O objetivo é, a partir do ponto A, fazer a busca minuciosa no local até chegar ao ponto B.
Ainda com base na figura CG1A3-I e nas informações a ela pertinentes, considere que mais policiais tenham sido convocados para essa busca, de maneira que a equipe agora tenha 135 policiais. Além disso, considere que três caminhos tenham sido selecionados como os mais prováveis de se encontrar as drogas escondidas. Esses caminhos foram denominados de R, S e T. Foi dada a liberdade para que cada policial escolhesse quais caminhos percorrer e, ao final de 5 horas, todos retornaram ao ponto de encontro. O seguinte relatório foi compilado:
70 policiais percorreram o caminho S;
40 percorreram somente o caminho T;
30 percorreram somente os caminhos R e S;
20 percorreram somente os caminhos S e T; 10 percorreram
somente os caminhos R e T; e somente 10 percorreram os três caminhos.
Nessa situação hipotética, o número de policiais que percorreram somente o caminho R é igual a
Com velocidade média constante, em uma viagem de carro, Enzo fez um percurso de 500 km, da cidade A até a cidade B, em 6 horas e 15 minutos. Também com velocidade média constante, Maria Valentina fez o mesmo percurso de carro, porém no sentido oposto, em 8 horas e 20 minutos.
Com base nessa situação hipotética, julgue o item.
A razão entre os tempos de percurso de Enzo e Valentina é igual a 0,75.
Em uma festa com 15 (quinze) pessoas, considere as afirmações:

Está CORRETO o que se afirma em
Considere a seguinte sequência:
0 - (1/3) - (-9) - (1/27) - …
O sétimo item da sequência é:
Notação científica é uma maneira de escrever números muito grandes ou pequenos. Um número está escrito em notação científica quando temos um número entre 1 e 10 multiplicado por uma potência de 10. Por exemplo: o número 67.200.000 pode ser escrito na notação científica como 6,72.10^7 e o número 0,0023 pode ser escrito como 2,3.10^-3. Considere a seguinte equação:
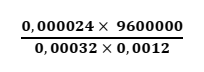
O resultado da equação acima em notação científica é:
O técnico deverá escolher 11 dentre 14 jogadoras para iniciar uma partida de futebol feminino. No vestiário há apenas meninas com 18, 19, 20, 21 e 22 anos. O número de meninas com 18 e com 20 anos é o mesmo e o número daquelas que têm 19 anos é 3 vezes o número das com 18 anos. Existem 3 meninas de 21 anos e só uma delas irá jogar. Uma das que tem 18 anos está machucada e não vai jogar e a única jogadora que tem 22 anos também é a única goleira. A soma das idades das 11 jogadoras que entrarão em campo é
Luciana é professora de italiano e dá aula de 14 em 14 dias, Domingos é professor de espanhol e dá aulas de 4 em 4 dias, e Ana é professora de francês e dá aulas de 7 em 7 dias. Os três dão aulas na mesma escola de línguas. Sabendo que deram aula no dia 29 de junho de 2022, a próxima data em que se encontrarão na escola para dar aula é
Considere um grande dado cúbico de madeira com seis faces numeradas de 1 a 6. Três formigas encontram-se paradas sobre a superfície desse dado de modo que:
- a formiga A está no ponto comum das faces com os números 1, 2 e 3;
- a formiga B está sobre a face com o número 1, posicionada de forma que sua distância até a formiga A seja a maior possível;
- a formiga C está sobre a face com o número 2, também posicionada de forma que sua distância até a formiga A seja a maior possível.
Se a distância entre as formigas A e B é de 40 cm, então a distância entre as formigas B e C, em centímetros, é de

