Supondo que Z seja uma distribuição normal padrão, considere as seguintes transformações de variáveis aleatórias: W = 1 - Z e V = Z2 - W2 + 1. A respeito dessas variáveis aleatórias, julgue o item a seguir.
A variância da variável aleatória V é igual a 2.
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Se o teste for efetuado com nível de significância igual a 1%, o poder do teste será igual a 99% para qualquer valor hipotético µ.
Considerando que X e Y sejam variáveis aleatórias mutuamente independentes que seguem distribuição normal padrão, julgue o próximo item.
A soma S = X + Y e a diferença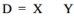 
seguem distribuições distintas.
Diversos processos buscam reparação financeira por danos morais. A tabela seguinte mostra os valores, em reais, buscados em 10 processos — numerados de 1 a 10 — de reparação por danos morais, selecionados aleatoriamente em um tribunal.
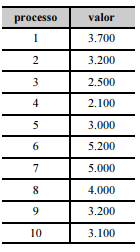
A partir dessas informações e sabendo que os dados seguem uma distribuição normal, julgue o item subsequente.
Caso seja de interesse testar, por exemplo, se a média dos valores é diferente de 3.500, para calcular o p-valor do teste no referido estudo é suficiente multiplicar a 
por 2, em que 
é a média amostral.
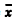
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que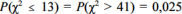 
, em que 
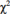representa a distribuição qui-quadrado com 25 de liberdade, e que 
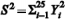, julgue o item a seguir.
A variância da distribuição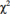 
, com 25 graus de liberdade é superior a 40.
Os tempos de duração de exames de cateterismo cardíaco ( Y, em minutos) efetuados por determinada equipe médica seguem uma distribuição normal com média µ e desvio padrão σ, ambos desconhecidos. Em uma amostra aleatória simples de 16 tempos de duração desse tipo de exame, observou-se tempo médio amostral igual a 58 minutos, e desvio padrão amostral igual a 4 minutos.
A partir da situação hipotética apresentada e considerando Φ(2) = 0,977, em que Φ(z) representa a função de distribuição acumulada de uma distribuição normal padrão e z é um desvio padronizado, julgue o item que se segue, com relação ao teste de hipóteses H0 = µ ≥ 60 minutos, contra HA = µ < 60 minutos, em que H0 e HA denotam, respectivamente, as hipóteses nula e alternativa.
Ao se aplicar o teste t de Student com nível de significância igual a 2,3%, conclui-se haver evidências estatisticamente significativas contra a hipótese H0.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que 
e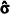 
representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
A razão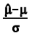 
segue uma distribuição normal padrão.
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que 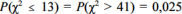, em que 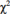representa a distribuição qui-quadrado com 25 de liberdade, e que 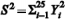, julgue o item a seguir.
A razão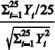 
segue uma distribuição t de Student com 24 graus de liberdade.
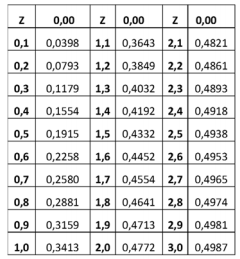
A variável normal padronizada Z é dada por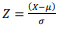 
, em que X é uma variável que tem distribuição normal de média μ e variância σ2, conforme a figura apresentada. Considerando uma variável X que tem distribuição normal de média μ = 15,6 e variância σ2 = 0,25, assinale a alternativa que indica a probabilidade p(15 < X < 16,2).
Dado: Tabela – Áreas de uma distribuição normal padrão
O valor diário (em R$ mil) apreendido de contrabando em determinada região do país é uma variável aleatória W que segue distribuição normal com média igual a R$ 10 mil e desvio padrão igual a R$ 4 mil.
Nessa situação hipotética,
a razão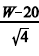 
segue distribuição normal padrão.
X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que e 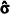representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
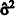é um estimador viciado (ou tendencioso) para a variância populacional, pois 
.
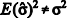X1, X2, ..., X10 representa uma amostra aleatória simples retirada de uma distribuição normal com média µ e variância σ2, ambas desconhecidas. Considerando que e 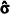representam os respectivos estimadores de máxima verossimilhança desses parâmetros populacionais, julgue o item subsecutivo.
O estimador de máxima verossimilhança para a função de densidade da distribuição normal em questão é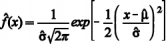 
, para qualquer valor real x.
Considerando que X e Y sejam variáveis aleatórias mutuamente independentes que seguem distribuição normal padrão, julgue o próximo item.
A soma dos quadrados Q = X2 + Y2 segue uma distribuição exponencial com média igual a 2.
Uma amostra aleatória simples
Y1, Y2, ..., Y25 foi retirada de uma distribuição normal com média nula e variância σ2, desconhecida. Considerando que 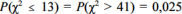, em que 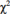representa a distribuição qui-quadrado com 25 de liberdade, e que 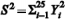, julgue o item a seguir.
[S 2/41;S2/13] representa um intervalo de 95% de confiança para a variância σ2.
Uma amostra aleatória simples X1, X2, ..., Xn foi retirada de uma
população normal com média e desvio padrão iguais a 10. Julgue
os próximos itens, a respeito da média amostral = [X1 + X2 + ... + Xn]/n.
A estatística
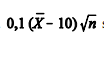
segue uma distribuição normal padrão.
