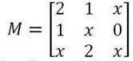Sabendo que as matrizes A e B têm ordem 3 e são tais que det(A) = 2 e det(B) = 3, assinale a alternativa que apresenta o valor de det(3A × 2B)
Os valores de x real que satisfazem à equação det = 0 pertencem ao conjunto
O valor do determinante da matriz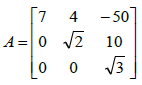
é:
Considere a matriz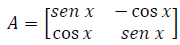 
e as seguintes proposições:
I- Se Paris está na França então o determinante de A é igual a 0 (zero).
II- Se Paris está na Inglaterra então o determinante de A é igual a 1 (um).
III- Se Paris está na França, então o determinante de A é igual a 1 (um).
IV- Se Paris está na Inglaterra, então o determinante de A é igual a 0 (zero).
Então, entre as quatro proposições acima, o rol completo da(s) proposição(ões) correta(s) é:
Seja a matriz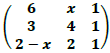 
. Determine a soma dos valores de x que fazem o determinante dessa matriz ser nulo.
Considere as matrizes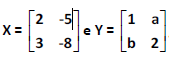 
, onde X e Y possuem o mesmo determinante e a e b são números inteiros positivos com a > b. Então, o valor de 3a – b é:
Se M é uma matriz quadrada de ordem 2 e N uma matriz quadrada de ordem 3, tal que 2 ∙ det M + det N = –1, então o valor de det (4M) + det (2N) é:
Uma professora de matemática solicitou aos seus alunos que encontrassem o determinante da matriz M=
. O valor encontrado foi:
O determinante da matriz 
é:
Considere as matrizes A e B, quadradas de ordem 2, com det A = 10 e det B = 2. Então o valor de det [(4.A) .(3.B) ] é igual:
As matrizes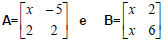 
possuem o mesmo determinante. Então o valor de x que aparece na matriz A e na matriz B é igual a:
Considere a matriz quadrada A, de ordem 2, definida por:
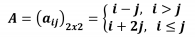
O determinante dessa matriz A será igual a
O valor do determinante da matriz quadrada de ordem 2 cujo produto dos elementos da diagonal principal é igual a 10 e o produto dos elementos da diagonal secundária é igual a (- 4) ,é:
Seja a matriz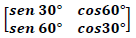 
, o valor de seu determinantes é:
Considere a matriz
e ainda que det M é o determinante da matriz M. Dessa forma, pode-se afirmar que a equação det M = 2 tem raízes cuja soma é igual a:
